Задачи и упражнения. 1.1.Из генеральной совокупности (y, x(1), , x(p)), где y имеет нормальный закон распределения с условным математическим ожиданием и дисперсией s2
1.1. Из генеральной совокупности (y, x (1),..., x (p)), где y имеет нормальный закон распределения с условным математическим ожиданием
1.2. По условию задачи 1.1 найти математическое ожидание суммы квадратов отклонений, обусловленных регрессией, т.е. EQR, где
1.3. По условию задачи 1.1 определить математическое ожидание суммы квадратов отклонений, обусловленных остаточной вариацией относительно линий регрессии, т.е. EQ ост, где
1.4. Доказать, что при выполнении гипотезы Н0: q=0 статистика
имеет F-распределение с числами степеней свободы n1=p+1 и n2=n-p-1.
1.5. Доказать, что при выполнении гипотезы Н0: qj=0 статистика
1.6. На основании данных (табл.1.4) о зависимости усушки кормового хлеба (y) от продолжительности хранения (x) найти точечную оценку условного математического ожидания в предположении, что генеральное уравнение регрессии - линейное.
Таблица 1.4.
Требуется: а) найти оценки
1.7. На основании данных о динамике темпов прироста курса акций за 5 месяцев, приведенных в табл. 1.5. Таблица 1.5.
и предположения, что генеральное уравнение регрессии имеет вид в) с надежностью g=0, 95 найти интервальные оценки параметров q0 и q1; г) с надежностью g=0, 9 установить интервальную оценку условного математического ожидания
1.8. Результаты исследования динамики привеса молодняка приведены в табл.1.6. Таблица 1.6.
Предполагая, что генеральное уравнение регрессии - линейное, требуется: а) определить оценки в) с надежностью g=0, 8 найти интервальные оценки параметров q0 и q1; г) с надежностью g=0, 98 определить и сравнить интервальные оценки условного математического ожидания д) определить при g=0, 98 доверительный интервал предсказания
1.9. Себестоимость (y) одного экземпляра книги в зависимости от тиража (x) (тыс.экз.) характеризуется данными, собранными издательством (табл.1.7). Определить МНК-оценки Таблица 1.7.
1.10. Данные о расходе электроэнергии (кВт/ч) на изготовление одной тонны цемента (y) в зависимости от объема выпуска (x) продукции (тыс.т) цементными заводами приводятся в табл. 1.8. Таблица 1.8.
Определить оценки
1.11. В табл. 1.9 представленные данные о темпах прироста (%) следующих макроэкономических показателей n =10 развитых стран мира за 1992г.: ВНП - x (1), промышленного производства - x (2), индекса цен - x (3). Таблица 1.9.
Примем за объясняемую величину (у) показатель x (1), а за объясняющую (х) переменную x (2) и предположим, что уравнение регрессии имеет вид: 1. 2. 3. Требуется: а) определить (с учетом линеаризации уравнения) МНК-оценки
1.12. Задачу 1.11 решить, приняв за объясняемую величину (у) показатель x (1), а за объясняющую (х) переменную x (3).
Тест 1. Какие требования в модели регрессионного анализа предъявляются к распределению ошибок наблюдения e i, а именно к их математическому ожиданию Me i и дисперсии De i: а) Me i =1; De i =s2; б) Me i =0; De i =0; в) Me i =0; De i =s2; г) Me i =1; De i =0.
2. Что минимизируется согласно методу наименьших квадратов: а) б) в) г)
3. Дана ковариационная матрица вектора
Чему равна оценка дисперсии элемента q2 вектора q, т.е. а) 5, 52; б) 0, 04; в) 0, 01; г) 2, 21.
4. При исследовании зависимости себестоимости продукции у от объема выпуска х 1 и производительности труда х 2 по данным n =20 предприятий получено уравнение регрессии: а) q1; б) q2; в) оба значимы; г) оба не значимы.
5. По данным теста 4 определите с доверительной вероятностью g=0, 99 на какую величину максимально может измениться себестоимость продукции у, если объем производства х 1 увеличить на единицу: а) -0, 6; б) 0, 72; в) -1, 5; г) -0, 83.
6. По данным теста 4 определите на сколько процентов в среднем изменится себестоимость продукции у, если производительность труда х 2 увеличить на 1%, учитывая при этом а) 0, 101%; б) -0, 101%; в) -0, 404%; г) 0, 404%.
7. Уравнению регрессии а) 70, 6; б) 16, 0; в) 84, 0; г) 29, 4.
8. По данным n =15 фирм исследована зависимость прибыли у от числа работающих х вида
Определите чему равна дисперсия оценки коэффициента регрессии а) 1, 500; б) 0, 110; в) 0, 682; г) 0, 242.
9. По данным n =25 регионов получена регрессионная модель объема реализации медикаментов на одного жителя у в зависимости от доли городского населения х 1 и числа фармацевтов х 2 на 10 тыс. жителей: а) 0, 3; б) 0, 2; в) 0, 1; г) 0, 05.
10. По данным теста №9 определите, чему равна при доверительной вероятности g=0, 95 верхняя граница интервальной оценки коэффициента регрессии при х 2: а) 0, 13; б) 0, 2; в) 0, 65; г) 0, 71.
|

 и дисперсией s2, взята случайная выборка объемом n, и пусть (yi, xi (1),..., xi (p)) - результат i -го наблюдения (i =1, 2,..., n). Определить: а) математическое ожидание МНК-оценки
и дисперсией s2, взята случайная выборка объемом n, и пусть (yi, xi (1),..., xi (p)) - результат i -го наблюдения (i =1, 2,..., n). Определить: а) математическое ожидание МНК-оценки 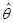 вектора q; б) ковариационную матрицу МНК-оценки
вектора q; б) ковариационную матрицу МНК-оценки  .
. .
. .
.
 имеет t-распределение с числом степеней свободы n=n-p-1.
имеет t-распределение с числом степеней свободы n=n-p-1. и остаточной дисперсии s2 в предположении, что генеральное уравнение регрессии имеет вид
и остаточной дисперсии s2 в предположении, что генеральное уравнение регрессии имеет вид  ; б) проверить при a=0, 05 значимость уравнения регрессии, т.е. гипотезу Н0: q=0; в) с надежностью g=0, 9 определить интервальные оценки параметров q0, q1; г) с надежностью g=0, 95 определить интервальную оценку условного математического ожидания
; б) проверить при a=0, 05 значимость уравнения регрессии, т.е. гипотезу Н0: q=0; в) с надежностью g=0, 9 определить интервальные оценки параметров q0, q1; г) с надежностью g=0, 95 определить интервальную оценку условного математического ожидания  при х 0=6; д) определить при g=0, 95 доверительный интервал предсказания
при х 0=6; д) определить при g=0, 95 доверительный интервал предсказания  в точке х =12.
в точке х =12. , требуется: а) определить оценки
, требуется: а) определить оценки  и
и  параметров уравнения регрессии и остаточной дисперсии s2; б) проверить при a=0, 01 значимость коэффициента регрессии, т.е. гипотезы H0: q1=0;
параметров уравнения регрессии и остаточной дисперсии s2; б) проверить при a=0, 01 значимость коэффициента регрессии, т.е. гипотезы H0: q1=0; в точке x =5.
в точке x =5. параметров уравнения регрессии и остаточной дисперсии s2; б) проверить при a=0, 05 значимость уравнения регрессии, т.е. гипотезы H0: q=0;
параметров уравнения регрессии и остаточной дисперсии s2; б) проверить при a=0, 05 значимость уравнения регрессии, т.е. гипотезы H0: q=0; , с надежностью g=0, 9 построить доверительные интервалы для параметров q0 и q1, а также условного математического ожидания
, с надежностью g=0, 9 построить доверительные интервалы для параметров q0 и q1, а также условного математического ожидания  .
. .
. остаточной дисперсии; б) проверить при a=0, 05 значимость коэффициента регрессии, т.е. Н0: q1=0; в) с надежностью g=0, 9 найти интервальные оценки q0 и q1; г) найти при g=0, 95 доверительный интервал для
остаточной дисперсии; б) проверить при a=0, 05 значимость коэффициента регрессии, т.е. Н0: q1=0; в) с надежностью g=0, 9 найти интервальные оценки q0 и q1; г) найти при g=0, 95 доверительный интервал для  ;
; ;
; ;
;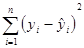 .
.

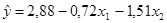 и среднеквадратические отклонения коэффициентов регрессии:
и среднеквадратические отклонения коэффициентов регрессии:  и
и  . Можно ли при уровне значимости a=0, 05 утверждать, что значимы коэффициенты регрессии:
. Можно ли при уровне значимости a=0, 05 утверждать, что значимы коэффициенты регрессии: ,
,  и
и  :
: соответствует множественный коэффициент корреляции
соответствует множественный коэффициент корреляции  . Какая доля вариации результативного показателя у (в %) объясняется входящими в уравнение регрессии переменными х 1 и х 2:
. Какая доля вариации результативного показателя у (в %) объясняется входящими в уравнение регрессии переменными х 1 и х 2: . Была получена оценка остаточной дисперсии
. Была получена оценка остаточной дисперсии  и обратная матрица:
и обратная матрица:
 :
: и среднеквадратические отклонения коэффициентов регрессии
и среднеквадратические отклонения коэффициентов регрессии 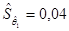 и
и  . Начиная с какого уровня значимости a можно утверждать, что у зависит от доли городского населения х 1:
. Начиная с какого уровня значимости a можно утверждать, что у зависит от доли городского населения х 1:


