Регрессионная модель производительности труда
По данным годовых отчетов десяти (n =10) машиностроительных предприятий провести регрессионный анализ зависимости производительности труда у (тыс. руб. на чел.) от объема производства х (млн.руб.). Предполагается линейная модель, т.е.
Таблица 1.1. Исходная информация для анализа и результаты расчетов
Решение: Определим вектор оценок
Воспользовавшись правилами умножения матриц будем иметь
В матрице
Найдем обратную матрицу
Тогда вектор оценок коэффициентов регрессии равен
а оценка уравнения регрессии будет иметь вид
Перейдем к статистическому анализу полученного уравнения регрессии: проверке значимости уравнения и его коэффициентов, исследованию абсолютных Предварительно определим вектор модельных значений результативного показателя
Тогда
А несмещенная оценка остаточной дисперсии равна:
а оценка среднеквадратического отклонения
Проверим на уровне значимости a=0, 05 значимость уравнения регрессии, т.е гипотезу H0: q=0 (q0=q1=0). Для этого вычисляем величину
По таблице F-распределения для a=0, 05, n1=2 и n2=8 находим Fкр=4, 46. Так как Fнабл> Fкр, то уравнение является значимым. Найдем оценку ковариационной матрицы вектора
Отсюда получаем несмещенные оценки дисперсий и среднеквадратических отклонений коэффициентов регрессии:
Для проверки значимости коэффициента регрессии, т.е. гипотезы Н0: q1=0, находим по таблице t-распределения при a=0, 05, n=8 значение tкр=2, 31:
Так как Определим интервальные оценки коэффициентов уравнения с доверительной вероятностью g=0, 95. Т.к.
где j=0; 1, то q0Î [0, 525 ± 2, 31´ 0, 391], откуда -0, 378 £ q0 £ 1, 428 и q1Î [0, 74861 ± 2, 31´ 0, 0428], откуда 0, 650 £ q1 £ 0, 847. Приведенные неравенства подтверждают вывод о значимости q1 (q1¹ 0). В то же время коэффициент q0 уравнения (1.2) не значим (границы доверительного интервала имеют разные знаки).
|

 .
.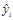
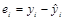
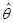 коэффициентов регрессии. Согласно методу наименьших квадратов, вектор b получается из выражения:
коэффициентов регрессии. Согласно методу наименьших квадратов, вектор b получается из выражения: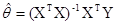 (1.1)
(1.1)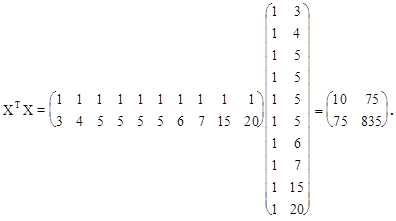
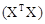 число 10, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы ХТ и 1-го столбца матрицы Х, а число 75, лежащее на пересечении 1-й строки и 2-го столбца - как сумма произведений элементов 1-й строки матрицы ХТ и 2-го столбца матрицы Х и т.д.
число 10, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы ХТ и 1-го столбца матрицы Х, а число 75, лежащее на пересечении 1-й строки и 2-го столбца - как сумма произведений элементов 1-й строки матрицы ХТ и 2-го столбца матрицы Х и т.д.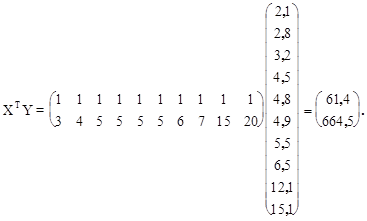
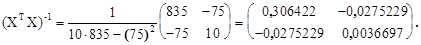
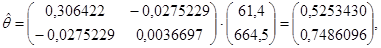
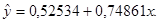 (1.2)
(1.2)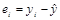 и относительных
и относительных 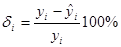 ошибок аппроксимации.
ошибок аппроксимации. :
: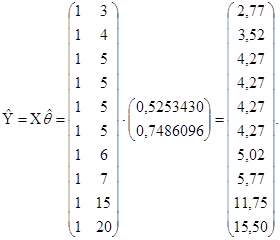
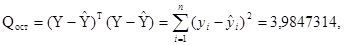 (1.3)
(1.3)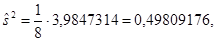
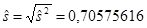 .
.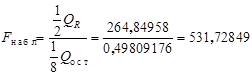 (1.4)
(1.4)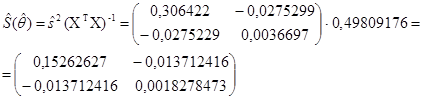 (1.5)
(1.5)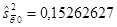
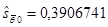
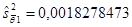
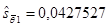
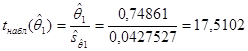 (1.6)
(1.6)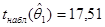 больше tкр=2, 31, то коэффициент регрессии q1 значимо отличается от нуля. Таким образом, окончательное уравнение регрессии имеет вид
больше tкр=2, 31, то коэффициент регрессии q1 значимо отличается от нуля. Таким образом, окончательное уравнение регрессии имеет вид 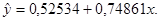
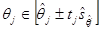 (1.7)
(1.7)


