Исходные (xt) и расчетные значения количества родившихся
по кварталам (1994-1995гг.)
Требуется определить расчетные значения и прогноз (при t =9) количества родившихся, воспользовавшись моделью экспоненциального сглаживания с мультипликативной сезонностью и линейным ростом (модель Уинтерса) при периоде упреждения t=1 и параметрах адаптации a1=0, 2; a2=0, 3 и a3=0, 4.
Модель экспоненциального сглаживания с мультипликативной сезонностью и линейным ростом (модель Уинтерса)
Напомним, что сезонная модель с линейным ростом Уинтерса имеет вид:
где хt — исходный временной ряд t =1, 2,..., n; a 1, t — параметр, характеризующий линейную тенденцию развития процесса, т.е. средние значения уровня исследуемого временного ряда хt в момент t; f n tkt — коэффициент сезонности для n t -й фазы kt -го цикла; n t =1, 2,..., l; где n t = t ‑ l× (kt ‑ 1); l — число фаз в полном цикле (в месячных временных рядах l =12, в квартальных — l =4 и т.д.); e t — случайная ошибка. Обычно предполагается, что вектор eÎ Nn (0, s2 I n), где e=(e1,..., e t,..., e n)T; I n — единичная матрица размерности (n ´ n). Адаптивные параметры модели (3.11) оцениваются с помощью рекуррентной экспоненциальной схемы по данным временного ряда xt, состоящего из n наблюдений:
где a 2, t — прирост среднего уровня ряда от момента t ‑ 1 к моменту t;
a1, a2 и a3 — параметры адаптации экспоненциального сглаживания (0< a1, a2, a3< 1). При этом, увеличение a j (j =1, 2, 3) ведет к увеличению веса более поздних наблюдений, а уменьшение a j — к улучшению сглаживания случайных отклонений. Эти два требования находятся в противоречии и поиск компромиссного сочетания значений a1, a2 и a3 составляет задачу оптимизации модели. Как следует из (3.12) экспоненциальное выравнивание всегда требует предыдущей оценки сглаживаемой величины. Когда процесс адаптации только начинается, то должны быть начальные значения, предшествующие первому наблюдению. В нашей задаче предстоит определить начальные условия: Таким образом, расчетные значения Решение. Первоначально по n =8 наблюдениям временного ряда xt найдем МНК-оценку линейного тренда
Определим начальные условия:
Мультипликативные коэффициенты сезонности нулевого цикла:
Расчеты будем проводить при параметрах адаптации a1=0, 2; a2=0, 3; a3=0, 4 и периоде упреждения t=1. Расчетные значения для 1-го цикла (kt =1, n t = t)
при t =1 согласно (3.12) имеем
при t =2
при t =3
при t =4
Расчетные значения для 2-го цикла (kt =2, n t = t -4) Здесь нам понадобятся коэффициенты сезонности, найденные для 1-го цикла: при t =5
Т.к.
при t =6
при t =7
при t =8
при t =9 (прогноз)
Полученные расчетные значения и прогноз
Рис. 3.4. Исходный ряд xt и его оценки
Заслуживает внимание сопоставление статистических характеристик трендовой модели Из приведенных характеристик и рис. 3.4 следует, что модель экспоненциального сглаживания с мультипликативной сезонностью Уинтерса более предпочтительна.
3.3. Прогнозирование объема производства железобетонных конструкций по модели Тейла-Вейджа В табл. 3.3 представлены данные (xt) об объеме производства в России сборных железобетонных конструкций по кварталам за 1994 и 1995 гг. (млн. куб. м.). Таблица 3.3.
|




 (3.11)
(3.11) (3.12)
(3.12) — расчетное значение временного ряда, определяемое для момента времени t с периодом упреждения t, т.е. по данным момента (t‑ t);
— расчетное значение временного ряда, определяемое для момента времени t с периодом упреждения t, т.е. по данным момента (t‑ t); где n t =1, 2,..., l.
где n t =1, 2,..., l. и
и 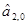 обычно уменьшается быстрее, чем
обычно уменьшается быстрее, чем  , т.к.
, т.к.  и
и  пересматриваются на каждом шаге, а
пересматриваются на каждом шаге, а  только один раз за цикл.
только один раз за цикл. . В результате расчета имеем:
. В результате расчета имеем: .
.
 — определим как среднюю арифметическую индексов сезонности
— определим как среднюю арифметическую индексов сезонности  -й фазы в исходном временном ряду:
-й фазы в исходном временном ряду:








 и
и  .
.
 относится ко 2-му циклу (kt =2), при выборе
относится ко 2-му циклу (kt =2), при выборе  исходили, что nt=5-4=1.
исходили, что nt=5-4=1.








 . Эти модели характеризуются значениями остаточных среднеквадратических отклонений относительно исходного временного ряда xt и соответственно равны
. Эти модели характеризуются значениями остаточных среднеквадратических отклонений относительно исходного временного ряда xt и соответственно равны  и
и  , а также средними относительными ошибками аппроксимации
, а также средними относительными ошибками аппроксимации  и
и  .
.


