Исходные и расчетные значения объема производства по кварталам
Требуется по модели экспоненциального сглаживания с аддитивной сезонностью и линейным ростом (модель Тейла-Вейджа) определить расчетные значения Модель экспоненциального сглаживания с аддитивной сезонностью и линейным ростом (модель Г. Тейла и С. Вейджа). Аддитивная модель, кроме самостоятельного значения в экономических исследованиях, интересна и тем, что позволяет строить модель с мультипликативной сезонностью и экспоненциальной тенденцией. Для этого необходима замена значений первоначального временного ряда их логарифмами, что преобразует экспоненциальную тенденцию в линейную и одновременно мультипликативную сезонную модель в аддитивную. Пусть наблюдение xt относится к nt-й фазе kt -го цикла, где n t = t‑ l× (kt -1) и l — число фаз в цикле (для квартального временного ряда l =4, а для месячного l =12). Модель с аддитивной сезонностью и линейным ростом можно представить в виде
где a 1, t — среднее значение уровня временного ряда в момент времени t после исключения сезонных колебаний; a2, t — аддитивный коэффициент роста от момента t ‑ 1 к моменту t;
e t — белый шум. Оценки параметров модели (3.13) будем искать при коэффициентах сглаживания a1, a2 и a3, где 0< a1, a2, a3< 1, по следующим процедурам адаптации:
где Начальные условия экспоненциального сглаживания определяют по исходному временному ряду xt (t =1, 2,..., n). Находим МНК-оценку линейного уравнения регрессии
и примем Решение. Первоначально по временному ряду xt, содержащему n =8 наблюдений, находим
Откуда В табл. 3.3 представлены расчетные значения
Расчеты проведем при параметрах адаптации a1=0, 1; a2=0, 4; a3=0, 3 и периоде упреждения t=1. Расчет модельных значений по 1994 г (Первый цикл: n t = t; kt =1; t=1) Исходные данные для расчета: При t =1 согласно (3.14) имеем:
При t =2
При t =3
При t =4
Расчет значений за 1995 г. (Второй цикл: n t = t -4; kt =2) Исходные данные для расчета: При t =5. При расчете 2-му циклу (k 5=2), поэтому n5= t-l (k 5-1)=5-4(2-1)=1 и
При t =6
При t =7
При t=8
При расчете прогнозного значения
Рассчитанные по модели Тейла-Вейджа, значения временного ряда
Рис. 3.5 Исходные xt и расчетные
Как уже отмечалось, если с учетом модели (3.13) предположить, что zt = ln(xt) и zt = a1t+gt+et1, то относительно xt имеем модель экспоненциального сглаживания с мультипликативной сезонностью и экспоненциальным ростом
Тогда исходному временному ряду xt ставится в соответствие расчетные значения В нашем примере, если предположить, что исходным является временной ряд z t = ln (xt), представленный в табл. 3.3, то
|




 (zt)
(zt)
 и прогноз при t =9, приняв период упреждения t=1, а параметры адаптации равными a1=0, 1; a2=0, 4 и a3=0, 3.
и прогноз при t =9, приняв период упреждения t=1, а параметры адаптации равными a1=0, 1; a2=0, 4 и a3=0, 3. (3.13)
(3.13) — аддитивный коэффициент сезонности для n t -й фазы kt -го цикла;
— аддитивный коэффициент сезонности для n t -й фазы kt -го цикла; (3.14)
(3.14) ‑ расчетное значение временного ряда, определяемое для момента времени t с упреждением t, т.е. по данным момента (t ‑ t).
‑ расчетное значение временного ряда, определяемое для момента времени t с упреждением t, т.е. по данным момента (t ‑ t).
 . В качестве оценок
. В качестве оценок  принимают средние значения отклонений
принимают средние значения отклонений  , соответствующих n t -й фазе исходного временного ряда, где n t =1, 2,..., l.
, соответствующих n t -й фазе исходного временного ряда, где n t =1, 2,..., l.
 .
.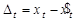 . Тогда начальные значения аддитивных коэффициентов сезонности равны:
. Тогда начальные значения аддитивных коэффициентов сезонности равны:

 .
.





 учитывается, что 5-я точка относится ко
учитывается, что 5-я точка относится ко . Тогда
. Тогда



 учитывалось, что момент t =9 принадлежит 3-му циклу, поэтому k 9‑ 1=2 и n9=9-4× 2=1, а
учитывалось, что момент t =9 принадлежит 3-му циклу, поэтому k 9‑ 1=2 и n9=9-4× 2=1, а  . Тогда
. Тогда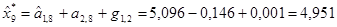

 .
. .
.


