Полиномиальные модели курса акций
В табл. 3.1 представлен временной ряд xt курса акций компании IBM (в долл.), включающий n =30 наблюдений. Приняв коэффициент адаптации a=0, 5 и период упреждения t=1, требуется аппроксимировать ряд xt с помощью адаптивной полиномиальной модели: а) нулевого порядка (p =0); б) первого порядка (p =1); в) второго порядка (p =2); г) рассчитать прогнозные значения при t =31; д) сравнить адекватность моделей по величине остаточного среднеквадратического отклонения  . .
Таблица 3.1.
Курс акций компаний IBM (в долл.) xt и расчеты по адаптивным полиномиальным моделям нулевого (p =0), первого (p =1)
и второго (p =2) порядков
|
|
| p =0
| p =1
| p =2
| | t
| xt
| S t
| 
| S t
| S t [2]
| 
| S t
| S t [2]
| S t [3]
| 
| |
|
| 506, 0
|
| 490, 6
| 489, 1
|
| 507, 2
| 508, 7
| 510, 3
|
| |
|
| 508, 0
| 506, 0
| 500, 3
| 494, 7
| 493, 6
| 508, 6
| 508, 6
| 509, 5
| 504, 9
| |
|
| 502, 5
| 508, 0
| 498, 6
| 496, 7
| 511, 5
| 502, 8
| 505, 7
| 507, 6
| 511, 8
| |
|
| 503, 2
| 502, 5
| 501, 3
| 499, 0
| 502, 6
| 503, 4
| 504, 6
| 506, 1
| 492, 8
| |
|
| 506, 6
| 503, 2
| 505, 7
| 502, 3
| 506, 0
| 506, 7
| 505, 7
| 505, 9
| 502, 5
| |
|
| 507, 8
| 506, 6
| 507, 3
| 504, 8
| 512, 5
| 507, 9
| 506, 8
| 506, 3
| 513, 9
| |
|
| 505, 4
| 507, 8
| 505, 2
| 505, 0
| 512, 3
| 505, 4
| 506, 1
| 506, 2
| 512, 5
| |
|
| 502, 7
| 505, 4
| 502, 6
| 503, 8
| 505, 6
| 502, 7
| 504, 4
| 505, 3
| 501, 7
| |
|
| 501, 4
| 502, 7
| 501, 3
| 502, 5
| 500, 2
| 501, 4
| 502, 9
| 504, 1
| 496, 1
| |
|
| 500, 7
| 501, 4
| 500, 6
| 501, 6
| 498, 9
| 500, 7
| 501, 8
| 503, 0
| 497, 2
| |
|
| 497, 8
| 500, 7
| 497, 8
| 499, 7
| 498, 6
| 497, 8
| 499, 8
| 501, 4
| 498, 9
| |
|
| 495, 9
| 497, 8
| 495, 9
| 497, 8
| 494, 0
| 495, 9
| 497, 8
| 499, 6
| 492, 2
| |
|
| 497, 5
| 495, 9
| 497, 5
| 497, 6
| 492, 1
| 497, 5
| 497, 7
| 498, 6
| 491, 7
| |
|
| 499, 7
| 497, 5
| 499, 7
| 498, 7
| 497, 3
| 499, 7
| 498, 7
| 498, 7
| 499, 9
| |
|
| 504, 4
| 499, 7
| 504, 4
| 501, 5
| 501, 7
| 504, 4
| 501, 6
| 500, 1
| 505, 7
| |
|
| 514, 7
| 504, 4
| 514, 7
| 508, 1
| 510, 2
| 514, 7
| 508, 1
| 504, 1
| 515, 2
| |
|
| 513, 3
| 514, 7
| 513, 3
| 510, 7
| 527, 9
| 513, 3
| 510, 7
| 507, 4
| 538, 3
| |
|
| 511, 7
| 513, 3
| 511, 7
| 511, 2
| 518, 5
| 511, 7
| 511, 2
| 509, 3
| 515, 7
| |
|
| 508, 8
| 511, 7
| 508, 8
| 510, 0
| 512, 7
| 508, 8
| 510, 0
| 509, 7
| 507, 1
| |
|
| 511, 9
| 508, 8
| 511, 9
| 511, 0
| 506, 4
| 511, 9
| 511, 0
| 510, 3
| 500, 4
| |
|
| 517, 0
| 511, 9
| 517, 0
| 514, 0
| 513, 7
| 517, 0
| 514, 0
| 512, 2
| 514, 5
| |
|
| 520, 0
| 517, 0
| 520, 0
| 517, 0
| 523, 0
| 520, 0
| 517, 0
| 514, 6
| 527, 8
| |
|
| 523, 5
| 520, 0
| 523, 5
| 520, 2
| 526, 0
| 523, 5
| 520, 2
| 517, 4
| 528, 4
| |
|
| 523, 2
| 523, 5
| 523, 2
| 521, 7
| 530, 1
| 523, 2
| 521, 7
| 519, 5
| 532, 1
| |
|
| 525, 6
| 523, 2
| 525, 6
| 523, 7
| 526, 2
| 525, 6
| 523, 7
| 521, 6
| 523, 4
| |
|
| 527, 3
| 525, 6
| 527, 3
| 525, 5
| 529, 4
| 527, 3
| 525, 5
| 523, 6
| 528, 6
| |
|
| 532, 7
| 527, 3
| 532, 7
| 529, 1
| 530, 9
| 532, 7
| 529, 1
| 526, 3
| 530, 5
| |
|
| 535, 8
| 532, 7
| 535, 8
| 532, 4
| 539, 9
| 535, 8
| 532, 4
| 529, 4
| 543, 1
| |
|
| 538, 4
| 535, 8
| 536, 4
| 535, 4
| 542, 6
| 538, 4
| 535, 4
| 532, 4
| 544, 2
| |
|
| 540, 7
| 538, 4
| 540, 7
| 538, 0
| 538, 4
| 540, 7
| 538, 1
| 535, 2
| 544, 4
| |
|
| 540, 9
| 540, 7
| 540, 8
| 539, 5
| 546, 1
| 540, 9
| 539, 5
| 537, 4
| 544, 7
| |
| Прогноз
| 540, 9
| 541, 0
| 540, 9
|
Решение. а) Адаптивная полиномиальная модель нулевого порядка (p=0).
экспоненциальная средняя имеет вид
S t = a xt + bSt-1, b = 1 - a.
Начальное условие: 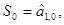 где за где за  примем среднее значение, например, первых пяти наблюдений. Для нашего примера примем среднее значение, например, первых пяти наблюдений. Для нашего примера 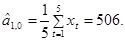
Расчетное модельное значение с периодом упреждения t будем определять из соотношения:
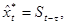 (3.1) (3.1)
Как уже отмечалось:  a=0, 5; t=1. a=0, 5; t=1.
Тогда
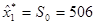
при t =1
S1 = a× x 1 + (1-a)S0 = 0, 5× 510 + 0, 5× 506 = 508
 , ,
при t =2
S1 = 0, 5× 497 + 0, 5× 508 = 502, 5
 , ,
при t =3
S1 = 0, 5× 504 + 0, 5× 502, 5 = 503, 65
 . .
Остальные результаты расчетов  где t =5, 6,..., 31 получены аналогично и приведены в табл. 3.1 (для модели (p =0)). где t =5, 6,..., 31 получены аналогично и приведены в табл. 3.1 (для модели (p =0)).
б) Адаптивная полиномиальная модель первого порядка (p =1).
Первоначально по данным временного ряда xt находим МНК-оценку линейного тренда:
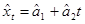
и принимаем  и и 
Экспоненциальные средние 1-го и 2-го порядков определяются как:
 (3.2) (3.2)
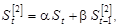
где b=1‑ a.
Отсюда начальные условия:
 (3.3) (3.3)
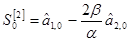
Оценка модельного значения ряда с периодом упреждения t равна:
 (3.4) (3.4)
Для нашего примера при a=0, 5 и t=1 имеем:
 (3.5) (3.5)
МНК-оценка уравнения тренда имеет вид:
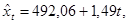
откуда  и и 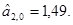
Согласно (3.3) получим:
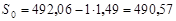
 . .
С учетом (3.5) найдем:
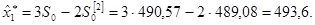
При t =1 экспоненциальные средние равны:
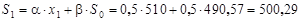
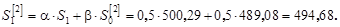
Откуда:
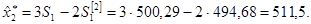
При t =2 имеем:
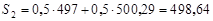
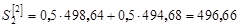
 . .
Остальные результаты расчетов  где t =4, 5,..., 31 получены аналогично и приведены в табл. 3.1 (для модели p =1). где t =4, 5,..., 31 получены аналогично и приведены в табл. 3.1 (для модели p =1).
в) Адаптивная полиномиальная модель второго порядка (p =2).
По данным временного ряда xt находим МНК—оценку параболического тренда
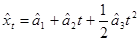
и экспоненциальные средние 1-го, 2-го и 3-го порядков:

Начальные условия определим как:
 (3.7) (3.7)
где  и и  . .
Оценка модельного значения с периодом упреждения t находим из выражения
 (3.8) (3.8)
Для нашего примера, когда a=b=0, 5 и t=1, выражения (3.7) и (3.8) преобразуются к виду
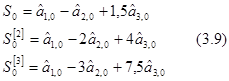
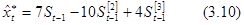
МНК-оценка уравнения тренда равна
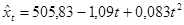
откуда:  . .
Согласно (3.9) получим начальные условия:
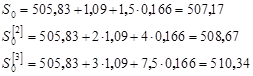
Из (3.10) следует:
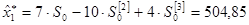
При t =1согласно (3.6) имеем

откуда из (3.10):
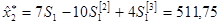
При t =2 с учетом (3.6):
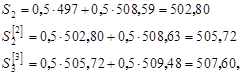
откуда согласно (3.10):
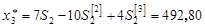 . .
При t =3 с учетом (3.6)
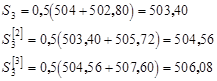
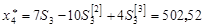
Остальные результаты расчетов при t =4, 5,..., 30 получены аналогично и приведены в табл. 3.1 (для модели p =2).
г) Прогнозные значения по адаптивным полиномиальным моделям равны (табл. 3.1):
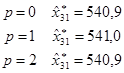
как видим они практически совпадают.
д) остаточные среднеквадратические отклонения  для моделей соответственно равны: 6, 3; 7, 4 и 8, 1. Из этого следует, что адаптивная полиномиальная модель нулевого порядка наиболее адекватна процессу xt. для моделей соответственно равны: 6, 3; 7, 4 и 8, 1. Из этого следует, что адаптивная полиномиальная модель нулевого порядка наиболее адекватна процессу xt.
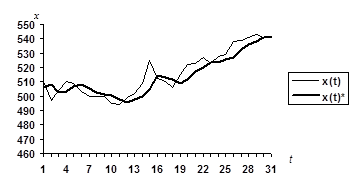
Рис. 3.1 Исходный (xt) и модельный  ряд курса акций IBM (долл.). Адаптивная полиномиальная модель 0-го порядка(p =0). ряд курса акций IBM (долл.). Адаптивная полиномиальная модель 0-го порядка(p =0).
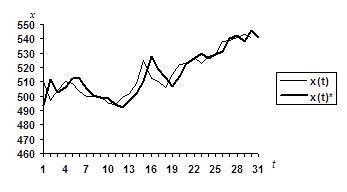
Рис. 3.2 Исходный (xt) и модельный  ряд курса акций IBM (долл.). Адаптивная полиномиальная модель 1-го порядка(p =1). ряд курса акций IBM (долл.). Адаптивная полиномиальная модель 1-го порядка(p =1).

Рис. 3.3 Исходный (xt) и модельный  ряд курса акций IBM (долл.). Адаптивная полиномиальная модель 2-го порядка(p =2). ряд курса акций IBM (долл.). Адаптивная полиномиальная модель 2-го порядка(p =2).
Однако сопоставляя исходные хt и модельные  значения временного ряда (рис. 3.1, 3.2 и 3.3) можно предположить, что прогностические свойства адаптивных полиномиальных моделей 1-го и 2-го порядка лучше, чем нулевого. Это следует из близости значений значения временного ряда (рис. 3.1, 3.2 и 3.3) можно предположить, что прогностические свойства адаптивных полиномиальных моделей 1-го и 2-го порядка лучше, чем нулевого. Это следует из близости значений  и и  в последних пяти точках временного ряда (при t =26¸ 30). На этом интервале остаточные среднеквадратические отклонения s для полиномиальных моделей нулевого (p =0), первого (p =1) и второго (p =2) порядков соответственно равны 6, 36; 4, 49 и 4, 45. В этой связи предпочтение следует отдать полиномиальной модели первого порядка, т.к. она проще и практически не отличается по точности от модели второго порядка. в последних пяти точках временного ряда (при t =26¸ 30). На этом интервале остаточные среднеквадратические отклонения s для полиномиальных моделей нулевого (p =0), первого (p =1) и второго (p =2) порядков соответственно равны 6, 36; 4, 49 и 4, 45. В этой связи предпочтение следует отдать полиномиальной модели первого порядка, т.к. она проще и практически не отличается по точности от модели второго порядка.

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
|

Теория усилителей. Схема Основная масса современных аналоговых и аналого-цифровых электронных устройств выполняется на специализированных микросхемах...
|

Логические цифровые микросхемы Более сложные элементы цифровой схемотехники (триггеры, мультиплексоры, декодеры и т.д.) не имеют...
|
Ситуация 26. ПРОВЕРЕНО МИНЗДРАВОМ
Станислав Свердлов закончил российско-американский факультет менеджмента Томского государственного университета...
Различия в философии античности, средневековья и Возрождения ♦Венцом античной философии было: Единое Благо, Мировой Ум, Мировая Душа, Космос...
Характерные черты немецкой классической философии 1. Особое понимание роли философии в истории человечества, в развитии мировой культуры. Классические немецкие философы полагали, что философия призвана быть критической совестью культуры, «душой» культуры.
2. Исследовались не только человеческая...
|
Деятельность сестер милосердия общин Красного Креста ярко проявилась в период Тритоны – интервалы, в которых содержится три тона. К тритонам относятся увеличенная кварта (ув.4) и уменьшенная квинта (ум.5). Их можно построить на ступенях натурального и гармонического мажора и минора.
...
Понятие о синдроме нарушения бронхиальной проходимости и его клинические проявления Синдром нарушения бронхиальной проходимости (бронхообструктивный синдром) – это патологическое состояние...
Опухоли яичников в детском и подростковом возрасте Опухоли яичников занимают первое место в структуре опухолей половой системы у девочек и встречаются в возрасте 10 – 16 лет и в период полового созревания...
|
|

 .
.
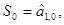 где за
где за  примем среднее значение, например, первых пяти наблюдений. Для нашего примера
примем среднее значение, например, первых пяти наблюдений. Для нашего примера 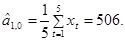
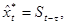 (3.1)
(3.1) a=0, 5; t=1.
a=0, 5; t=1.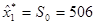
 ,
, ,
, .
. где t =5, 6,..., 31 получены аналогично и приведены в табл. 3.1 (для модели (p =0)).
где t =5, 6,..., 31 получены аналогично и приведены в табл. 3.1 (для модели (p =0)).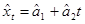
 и
и 
 (3.2)
(3.2)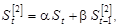
 (3.3)
(3.3)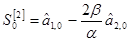
 (3.4)
(3.4) (3.5)
(3.5)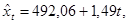
 и
и 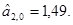
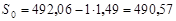
 .
.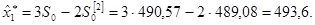
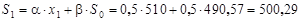
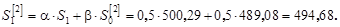
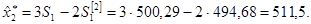
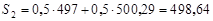
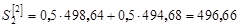
 .
.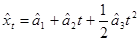

 (3.7)
(3.7) и
и  .
. (3.8)
(3.8)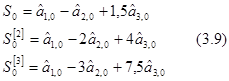
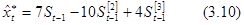
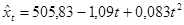
 .
.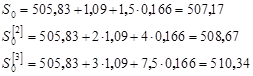
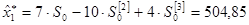

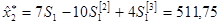
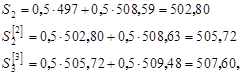
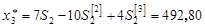 .
.
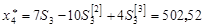
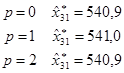

 ряд курса акций IBM (долл.). Адаптивная полиномиальная модель 0-го порядка(p =0).
ряд курса акций IBM (долл.). Адаптивная полиномиальная модель 0-го порядка(p =0).

 ряд курса акций IBM (долл.). Адаптивная полиномиальная модель 2-го порядка(p =2).
ряд курса акций IBM (долл.). Адаптивная полиномиальная модель 2-го порядка(p =2). и
и 


