Регрессионная модель объема продаж торгового дома, включающая линейную и гармонические составляющие

На основании данных (в млн.руб.) объема продаж торгового дома за n =12 месяцев (табл.2.3) построить регрессионную модель зависимости объема продаж от времени.

 

Таблица 2.3.

Данные объема продаж (млн.руб.)

месяц	t	yt
январь			241, 15	‑ 41, 15	201, 84	‑ 1, 84
февраль			252, 30	57, 69	303, 89	6, 11
март			263, 46	56, 53	323, 06	‑ 3, 06
апрель			274, 61	‑ 14, 61	258, 28	1, 71
май			285, 76	‑ 95, 76	192, 45	‑ 2, 45
июнь			296, 92	‑ 86, 92	209, 50	0, 49
июль			308, 07	1, 92	310, 49	‑ 0, 49
август			319, 23	90, 76	412, 54	‑ 2, 55
сентябрь			330, 38	99, 61	431, 71	‑ 1, 71
октябрь			341, 53	28, 46	366, 93	3, 06
ноябрь			352, 69	‑ 52, 69	301, 10	‑ 1, 10
декабрь			363, 84	‑ 43, 84	318, 16	1, 84

 

Графически временной ряд объема продаж торгового дома y_t и линейный тренд представлены на рис.2.2.

 

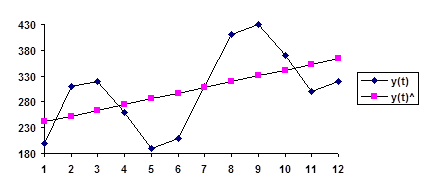
Рис.2.2. Временной ряд объема продаж y_t.

 

Решение. Первоначально аппроксимируем временной ряд линейным уравнением регрессии вида: .

Оценка уравнения регрессии, найденная с помощью метода наименьших квадратов имеет вид:

(2.7)

В скобках указаны оценки среднеквадратических отклонений коэффициентов уравнения (j =0, 1) Уравнение значимо и содержит все значимые по t -критерию коэффициенты q _j. Критическое значение t _kp=2, 23, найденное при a=2Q=0, 05 и n= n‑ 2=10, где Q ‑ процентная точка t -распределения, меньше расчетного .

Статистические характеристики уравнения: ; и DW=1, 01 свидетельствуют о наличии положительной коррелированности случайных остатков и о недостаточно хороших аппроксимирующих свойствах модели. Анализируя рис.2.2, где представлены графики y_t и , можно предположить наличие периодической (сезонной) составляющей временного ряда.

Для описания сезонных колебаний, представляющих собой циклический повторяющийся во времени процесс, может быть использован гармонический ряд (ряд Фурье) вида:

(2.8)

где ; ‑ угловая частота j -ой гармоники; j =1, 2,..., k ‑ номер гармоники; e _t ‑ случайная ошибка.

Из рис.2.2 видно, что обследуемый временной диапазон n =12 вмещает в себя два полных периода циклических колебаний анализируемого показателя. Отсюда можно предположить, что для адекватного описания v_t в (2.8) достаточно второй гармоники (j =2) с угловой частотой .

Первоначально включим в модель объема продаж две гармоники с угловыми частотами и w₂. Будем строить линейное уравнение регрессии относительно следующих переменных: t, , , и . В результате расчетов получим:

(2.9)

Уравнение (2.9) содержит два незначимых коэффициента регрессии, относящихся к 1-й гармонике (t _kp=2, 447 при a=0, 05 и n=6). Статистические характеристики уравнения (2.9) равны: ; ; и DW=3, 32. После реализации процедур в качестве окончательного было выбрано уравнение регрессии вида:

(2.10)

Все входящие в уравнение коэффициенты значимы, т.е. q_j¹ 0 (j =0, 1, 2, 3). Как видно из (2.10), расчетные значения больше критического значения t _kp=2, 306, найденного по таблице t -распределения при a=2Q=0, 05 и n=8, из чего следует, что гипотеза H₀: q _j =0 отвергается с вероятностью ошибки a=0, 05.

Уравнение (2.10) характеризуется остаточным среднеквадратическим отклонением ; множественным коэффициентом детерминации ; средней относительной ошибкой аппроксимации и статистикой Дарбина-Уотсона DW=3, 025, что свидетельствует об адекватности модели. Полученные характеристики особенно впечатляют при их сравнении с аналогичными параметрами модели (2.7).