Глава 5. Задачи и упражнения
5.1. Доказать, что если в регрессионной модели
5.2. По данным задачи 5.1 доказать, что ОМНК-оценка вектора q=(q0× q1)Т определяется по формуле
5.3. Пусть имеется l серий наблюдений, причем каждая i- я серия состоит из ni наблюдений (xij, yij), где i= 1, 2, …, l; j= 1, 2, …, ni, связанных соотношением
где Доказать, что если xi = xi1 = xi2 =… т.е. имеет место неравномерное дублирование наблюдений, то оценку параметров регрессионной модели
следует производить по обобщенному (взвешенному) МНК с матрицей весовых коэффициентов вида:
5.4. Доказать, что в условиях задачи 5.1 в обобщенном методе наименьших квадратов (ОМНК) ковариационная матрица вектора
5.5. При проведении актуарных расчетов компания, специализирующаяся на автотранспортном страховании, проанализировала n =20 произвольно отобранных страховых случаев, по каждому из которых фиксировались стоимость застрахованного автомобиля (х) и объем страховых возмещений (у). Данные наблюдений представлены в табл.5.1. Требуется определить и сравнить по точности МНК- и ОМНК-оценки параметров линейной модели регрессии При ОМНК-оценивании предполагается наличие гетероскедастичности, когда погрешности модели Таблица 5.1.
|

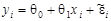
 , где Me i =0, De i =s2 и Me i e j =0 при i ¹ j, i, j =1, 2,..., n, то матрица весов в ОМНК имеет вид
, где Me i =0, De i =s2 и Me i e j =0 при i ¹ j, i, j =1, 2,..., n, то матрица весов в ОМНК имеет вид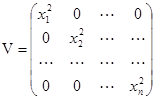
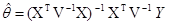 .
.

 ij,
ij, – взаимно некоррелированы и M
– взаимно некоррелированы и M  .
.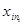 , а уi=
, а уi= 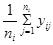 ,
,
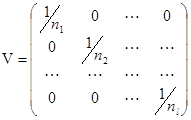
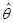 имеет вид
имеет вид 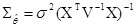 .
. .
. попарно независимы и
попарно независимы и 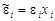 , где e i Î N(0, s2).
, где e i Î N(0, s2).


