Глава 6. Итоговый тест
1. Если эффективность производства не зависит от масштабов и оно описывается производственной функцией Кобба-Дугласа Q=A× Ka× LB, то с ростом параметра a параметр b: а) растет; в) остается неизменным; б) уменьшается; г) растет или уменьшается.
2. Если эффективность производства растет по мере его укрупнения и оно описывается производственной функцией Кобба-Дугласа, то параметры модели удовлетворяют соотношению: а) a+b< 1; в) a+b=0; б) a+b=1; г) a+b> 1.
3. В производственной функции Кобба-Дугласа параметр b соответствует коэффициенту: а) корреляции; в) эластичности; б) вариации; г) детерминации.
4. Получена производственная функция а) 0, 8; в) 0, 2; б) 2, 7; г) -0, 8.
5. Получены две производственные функции Кобба-Дугласа, имеющие равные значения параметров a и b, но различающиеся по параметру А. В каком случае первое производство более эффективно, чем второе: а) А1< А2; в) А1=А2; б) А1> А2; г) А1¹ А2.
6. Какие переменные называют предопределенными: а) экзогенные; в) лаговые; б) эндогенные; г) эгзогенные+лаговые.
7. Какая из систем регрессионных уравнений относится к рекурсивной модели: а) y 1, t=j1(x 1, t; y 2, t-1; x 2, t-1) в) y 1, t=j1(y 2, t; x 1, t; x 2, t-1) y 2, t=j2(y 1, t; x 1, t; x 2, t); y 2, t=j2(y 1, t; x t; x 2, t); б) y 1, t=j1(x 1, t; y 2, t; x 2, t-1) г) y 1, t=j1(x 1, t; y 2, t; x 1, t-1) y 2, t=j2(y 1, t; y 2, t-1; x 1, t); y 2, t=j2(y 1, t; x 1, t-1; x 2, t-2);
8. В чем состоит условие независимости погрешностей регрессионной модели а) б)
9. В чем состоит условие гомоскедастичности в регрессионной модели, если t1, t2=1, 2,..., n и t1¹ t2: а) б)
10. В чем состоит условие гетероскедастичности в регрессионной модели, если t1, t2=1, 2,..., n и t1¹ t2: а) б)
11. Как изменится в среднем объем производства q, описываемый производственной функцией
12. Какие методы используются при нахождении оценок параметров системы одновременных эконометрических уравнений?
Список рекомендуемой литературы 1. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики: Учебник. М., ЮНИТИ, 1998 (2-е издание 2001);
2. Айвазян С.А., Мхитарян В.С. Прикладная статистика в задачах и упражнениях: Учебник. М. ЮНИТИ – ДАНА, 2001;
3. Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика. Исследование зависимостей. М., Финансы и статистика, 1985, 487с.;
4. Айвазян С.А., Бухштабер В. М., Енюков И.С., Мешалкин Л.Д. Прикладная статистика. Классификация и снижение размерностей. М., Финансы и статисика, 1989, 607с.;
5. Джонстон Дж. Эконометрические методы, М.: Статистика, 1980, 446с.;
6. Дубров А.В., Мхитарян В.С., Трошин Л.И. Многомерные статистические методы. М., Финансы и статистика, 2000;
7. Мхитарян В.С., Трошин Л.И. Исследование зависимостей методами корреляции и регрессии. М., МЭСИ, 1995, 120с.;
8. Мхитарян В.С., Дубров А.М., Трошин Л.И. Многомерные статистические методы в экономике. М., МЭСИ, 1995, 149с.;
9. Дубров А.М., Мхитарян В.С., Трошин Л.И. Математическая статистика для бизнесменов и менеджеров. М., МЭСИ, 2000, 140с.;
10. Лукашин Ю.И. Регрессионные и адаптивные методы прогнозирования: Учебное пособие, М., МЭСИ, 1997.
11. Лукашин Ю.И. Адаптивные методы краткосрочного прогнозирования. ‑ М., Статистика, 1979.
|

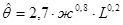 . Если объем капитала К увеличить на 1%, то объем производства в среднем изменится (в%) на:
. Если объем капитала К увеличить на 1%, то объем производства в среднем изменится (в%) на: и
и 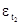 , где t1, t2=1, 2,..., n и t1¹ t2:
, где t1, t2=1, 2,..., n и t1¹ t2: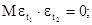 в)
в) 
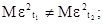 г)
г) 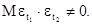
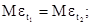 в)
в) 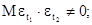
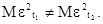
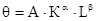 , если увеличить L на 1%, при неизмененном К?
, если увеличить L на 1%, при неизмененном К?


