Расчет теплообменника
Плотность теплового потока, проходящего от одной жидкости или газа к другой жидкости или газу через разделяющую их стенку, равна
tст1, tст2 - температура стенки со стороны горячего и холодного теплоносителя; tж1, tж2 – температура горячего и холодного теплоносителей; δ - толщина стенки; к – коэффициент теплопередачи, Вт/(м2 º С). Температурный напор представляет собой Δ t = tж1 – tж2. Средний температурный напор определяется по формуле Δ tср = Если Δ tср ≈ Для прямотока: Δ tмах = t'ж1 – t'ж2; Δ tмin = t''ж1 – t''ж2; Для противотока: Δ tмах = t'ж1 – t''ж2; Δ tмin = t''ж1 – t'ж2; где t'ж1, t''ж1 – начальная и конечная температура горячего теплоносителя; t'ж2, t''ж2 – начальная и конечная температура холодного теплоносителя. Коэффициенты теплоотдачи определяются по формуле α = где Nu – критерий Нуссельта; λ ж – коэффициент теплопроводности жидкости или газа, Вт/(м º С); l - характерный линейный размер, определяемый по формуле l = где Fс – площадь сечения потока; Пс – смоченный периметр сечения. Рассмотрим некоторые примеры сечений каналов.
Критерий Нуссельта зависит от режима течения жидкости и теплофизических свойств среды Nи = f (Rе, Рr), где критерий Рейнольдса равен Rе = и критерий Прандтля Рr = где ν – кинематическая вязкость среды, м2/с; μ – динамическая вязкость среды, Па ∙ с; с – удельная теплоемкость среды, Дж/(кг º С); λ ж – коэффициент теплопроводности среды, Вт/(м º С). По Михееву М.А. для ламинарного режима (Rе ≤ 2320) Nи = 0, 17Rе0, 33 Рr0, 43Gr0, 1 (Рr/ Рrст) 0, 25, где Рrст – критерий Прандтля при температуре стенки; Gr – критерий Грасгофа, равный Gr = β где β – температурный коэффициент объемного расширения жидкости или газа, К-1; Δ t – разность температур между стенкой и жидкостью на удалении от стенки; g – ускорение свободного падения (9, 81 м/с2); Для турбулентного режима (Rе > 10000): Nu = 0, 021Rе0, 8 Рr0, 43(Рr/ Рrст)0, 25, здесь (Рr/Рrст) 0, 25 – поправочный множитель, учитывающий направление теплового потока. При охлаждении жидкости (Рr/Рrст) 0, 25 ≈ 0, 95, а при нагреве (Рr/Рrст) 0, 25 ≈ 1, 05. Теплофизические свойства среды определяют для средних температур
Необходимая площадь поверхности теплообмена аппарата определяется по формуле F = где Qτ – тепловой поток (количество теплоты, проходящее в единицу времени) Qτ = В случае имеющегося осадка и пригара на стенке коэффициент теплопередачи определяется как к = где δ 1, δ 2 – толщина осадка (пригара) по обе стороны стенки, м; λ 1, λ 2 – коэффициент теплопроводности осадка (пригара) по обе стороны стенки, Вт/(м · град). Тепловой поток определяют исходя из уравнения теплового баланса Qτ = G1С1 (t¢ ж1 – t¢ ¢ ж1) = G2С2 (t¢ ¢ ж2 – t¢ ж2), где G1, G2 – массовые расходы соответственно горячего и холодного теплоносителей, кг/с; С1, С2 – удельные теплоемкости соответственно горячего и холодного теплоносителей. Из этого уравнения определяют и температуру (обычно конечную) одного из теплоносителей, например
Пусть G1 – массовый расход продукта (молока), тогда отношение n = называют кратностью агента. Для воды n = 2, 5 – 3, для рассола n = 1, 5 – 2, 5. Скорость движения среды в каналах
где ρ – плотность среды, кг/м3. Пример Определить площадь поверхности теплопередачи секции пастеризации теплообменника «труба в трубе» с вытеснительной вставкой, а также количество и длину труб, если производительность теплообменника по молоку составляет 2000 кг/ч. Начальная температура молока (при выходе из секции регенерации) составляет 55°С. Температура пастеризации должна быть 75°С. Молоко нагревается водой с температурой 95°С. Толщина стенки наружной трубы – 1 мм, внутренней – 1, 5 мм. В расчетах принять теплопроводность нержавеющей стали 14 Вт/ (м °С), пригар со стороны молока δ 1 = 0, 1 мм при λ 1 = 0, 3 Вт/ (м °С), пригар со стороны воды δ 2 = 0, 1 мм при λ 2 = 1, 74 Вт/ (м °С).
Рисунок 9.1 – Схема теплообменника «Труба в трубе» с вытеснительной вставкой
|

 Рисунок 9.1 – График теплопередачи через разделяющую стенку
Рисунок 9.1 – График теплопередачи через разделяющую стенку
 (tст1 – tст2) =α 2 (tст2 – tж2) = =к (tж1 – tж2),
где Q – количество переданной теплоты, Дж за время τ через площадь поверхности теплообмена F;
α 1, α 2 – коэффициенты теплоотдачи от жидкости (газа) к стенке, Вт/(м2º С);
λ – коэффициент теплопроводности стенки, Вт/(м ·º С);
(tст1 – tст2) =α 2 (tст2 – tж2) = =к (tж1 – tж2),
где Q – количество переданной теплоты, Дж за время τ через площадь поверхности теплообмена F;
α 1, α 2 – коэффициенты теплоотдачи от жидкости (газа) к стенке, Вт/(м2º С);
λ – коэффициент теплопроводности стенки, Вт/(м ·º С);
 .
. ≤ 2 можно принять
≤ 2 можно принять .
. ,
, ,
,
 ; Пс = π d; l =
; Пс = π d; l =  .
.

 .
.

 ; Пс = π (D + d);
l =
; Пс = π (D + d);
l =  = D – d = 2δ;.
= D – d = 2δ;.

 ,
,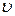 – средняя скорость движения среды;
– средняя скорость движения среды; Δ t,
Δ t, =
= 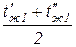 ;
;  =
=  .
.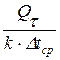 ,
, – для установившегося процесса.
– для установившегося процесса. ,
, .
.
 ,
,



