Задача 1 ( решение игры 2 x n)
Рассмотрим матричную игру, заданную платёжной матрицей первого игрока.
1. Проверим, есть ли у данной игры решение в области смешанных стратегий, т.е. есть ли у заданной матрицы седловая точка. a. Найдем нижнюю цену игры
b. Найдем верхнюю цену игры
c. Нижняя цена игры не равна верхнее цены игры, следовательно, седловой точки у заданной матрицы выигрышей нет и решения в чистых стратегиях отсутствует. Поэтому решение необходимо искать в области смешанных стратегий.
2. Данная игра 2 x 3 (или в общем случае 2 x n), следовательно необходимо строить прямые, соответствующие стратегиям второго игрока. Рассмотрим подробно алгоритм решения матричных игр графоаналитическим методом.
3. На плоскости хОy введём систему координат и на оси Ох отложим отрезок единичной длины А1, А2, каждой точке которого поставим в соответствие некоторую смешанную стратегию игрока 1 (х, 1 - х). В частности, точке А1 (0; 0) отвечает стратегия А1, точке А2 (1; 0) – стратегия А2 и т.д.
4. В точках А1 и А2 восстановим перпендикуляр и на полученных прямых будем откладывать выигрыш игроков. На первом перпендикуляре (в данном случае он совпадает с осью 0y) отложим выигрыш игрока 1 при стратегии А1, а на втором – при стратегии А2. Если игрок 1 применит стратегию А1, то выиграет при стратегии В1 игрока 2 – 2 (элемент a11 матрицы А), при стратегии В2– 3 (элемент a12 матрицы А), а при стратегии В3– 11 (элемент a13 матрицы А). Если же игрок 1 применит стратегию А2, то его выигрыш при стратегии В1 равен 7 (элемент a21 матрицы А), при В2– 5 (элемент a22 матрицы А), а при В3– 2 (элемент a23 матрицы А). Эти числа определены на перпендикуляре, восстановленном в точке А2. Соединив между собой точки соответствующие a11 и а21, а12 и а22, а13 и а23, получим три прямые, расстояние до которых от оси 0х определяет средний выигрыш при любом сочетании соответствующих стратегий. Например, расстояние от любой точки отрезка a11a21 до оси 0х определяет средний выигрыш u1 при любом сочетании стратегий А1 А2 (с частотами х и 1– х) и стратегией В1 игрока 2. Это расстояние равно 2 х1 + 6(1 - х2) = u1 5. Рассмотрим ломанную a11MNa23.
Таким образом, координаты точек, принадлежащих ломанной a11MNa23 определяют минимальный выигрыш игрока 1 при применении им любых смешанных стратегий. Эта минимальная величина является максимальной в точке N; следовательно этой точке соответствует оптимальная стратегия Х* =(p, 1- p), а её координата равна цене игры u. Координаты точки N находим как точку пересечения прямых а12а22 и а13а23. Соответствующие два уравнения имеют вид:
Проверка: цена игры
Это неравенство выполнено:
Следовательно, Х =
Оптимальные стратегии для игрока 2 можно найти, решив систему:
и, следовательно, Y = Значения p, q и u можно также вычислив, используя формулы (6), (7) и (9) для матрицы А*.
Ответ: Оптимальное решение находится в области смешанных стратегий. Оптимальная стратегия первого игрока X= Х =
|

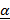 :
:
 :
: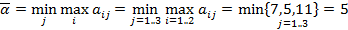



 должна удовлетворять следующему неравенству:
должна удовлетворять следующему неравенству:
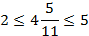
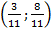 , при цене игры u =
, при цене игры u = 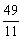 . Таким образом, мы можем найти оптимальную стратегию при помощи матрицы A*:
. Таким образом, мы можем найти оптимальную стратегию при помощи матрицы A*:
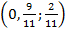 . (Из рисунка видно, что стратегия B1 не войдёт в оптимальную стратегию.
. (Из рисунка видно, что стратегия B1 не войдёт в оптимальную стратегию. .
.


