Задача 3. Решить задачу линейного программирования Симплекс методом:
Решить задачу линейного программирования Симплекс методом:
1. Приводим заданную систему ограничений к каноническому виду: Замечание: Задача ЛП в каноническом виде выглядит так:
Все ограничения должны быть типа «меньше или равно». После приведения системы к каноническому виду имеем:
2. Составляем первую укороченную симплекс-таблицу СТ1:
В столбце свободных членов есть отрицательные элементы, следовательно, необходимо применить “Алгоритм 2 Симплекс преобразования на основе укороченных симплекс таблиц” . 3. Выберем строку с наименьшим отрицательным свободным членом в B-столбце
Следовательно, s =2.
4. Рассмотрим элементы s-ой строки. Среди элементов s-ой строки есть отрицательный элемент - -1, следовательно, система совместна, и в качестве разрешающего столбца выбираем столбец, содержащий этот отрицательный элемент в s-ой строке:
5. Выбираем разрешающую строку k, которая соответствует наименьшему положительному из отношений элементов правой части уравнений на соответствующие элементы разрешающего столбца:
Минимальное отношение соответствует второй строке, следовательно, k=2.
6. Тогда элемент стоящий на пересечении разрешающего столбца и разрешающей строки называется разрешающим элементом
7. Далее выполняем все п.4 “Алгоритм 1 Симплекс преобразования на основе укороченных симплекс таблиц”.
Переходим к новой симплекс таблице СТ2 по следующим правилам: a. Меняем местами СП и БП соответствующие разрешающему элементу.
b. На месте разрешающего элемента в новой таблице стоит величина ему обратная:
c. Все элементы разрешающей строки делятся на разрешающее число, включая элемент последнего столбца:
d. Все элементы разрешающего столбца делятся на разрешающее число, включая элемент последней строки, с обратным знаком:
e. Все остальные элементы матрицы
Например, вычислим некоторые элементы таблицы:
Полученная СТ2 следующая:
8. Все элементы столбца свободных членов положительные, а в строке Z есть отрицательные элементы, следовательно, далее необходимо применить “Алгоритм 1 Симплекс преобразования на основе укороченных симплекс таблиц”. 9. Выбираем разрешающий столбец l соответствующий наименьшему отрицательному элементу в Z строке:
Следовательно,
10. Выбираем разрешающую строку k, которая соответствует наименьшему положительному из отношений элементов правой части уравнений (элементы столбца B) на соответствующие элементы разрешающего столбца:
Следовательно, 11. Тогда элемент стоящий на пересечении разрешающего столбца и разрешающей строки называется разрешающим элементом 12. Переходим к новой симплекс таблице СТ2 по следующим правилам: a. Меняем местами СП и БП соответствующие разрешающему элементу.
b. На месте разрешающего элемента в новой таблице стоит величина ему обратная:
c. Все элементы разрешающей строки делятся на разрешающее число, включая элемент последнего столбца:
d. Все элементы разрешающего столбца делятся на разрешающее число, включая элемент последней строки, с обратным знаком:
e. Все остальные элементы матрицы
Полученная СТ3 следующая:
13. В Z строке нет отрицательных элементов, следовательно, оптимальное решение найдено и максимум целевой функции
Ответ: Zmax=
|

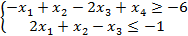




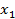
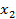

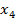
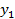





 3
3

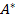 вычисляются по формулам:
вычисляются по формулам: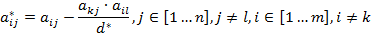
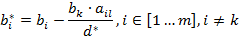
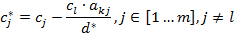
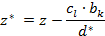







 , так как минимальное положительное отношение соответствует первой строке.
, так как минимальное положительное отношение соответствует первой строке.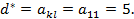











 для заданной системы ограничений равен
для заданной системы ограничений равен  при этом
при этом  ,
,  (см столбце свободных членов)
(см столбце свободных членов)


