Изначально имеем систему неравенств  и целевую функцию
и целевую функцию  , для которой необходимо определить максимум для заданной системы неравенств. Переменные
, для которой необходимо определить максимум для заданной системы неравенств. Переменные 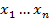 - Свободные Переменные (СП).
- Свободные Переменные (СП).
Чтобы свести неравенства к равенствам к левой части неравенств  добавляют некоторую неотрицательную величину
добавляют некоторую неотрицательную величину 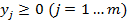 . Переменные
. Переменные  - Базисные Переменные (БП).
- Базисные Переменные (БП).
Тогда укороченная симплекс таблица примет вид:
| CП БП
| 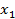
| …
| 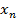
| B
|
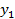
| 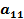
| …
| 
| 
|
| …
| …
| …
| …
| …
|

| 
| …
| 
| 
|
| Z
| 
| …
| 
|
|
Замечание 1:
Для дальнейшего удобства обозначим элемент в Z строке и B столбце  .
.
Замечание 2:
Данный алгоритм применим, если  .
.
- Выбирается разрешающий столбец l соответствующий наименьшему отрицательному элементу в Z строке
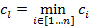
- Выбирается разрешающая строка k, которая соответствует наименьшему положительному из отношений элементов правой части уравнений на соответствующие элементы разрешающего столбца:
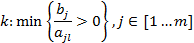
Замечание: Если все отношения 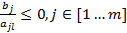 , значит, целевая функция Z неограниченно возрастает и решения нет. Необходимо прекратить симплекс преобразование.
, значит, целевая функция Z неограниченно возрастает и решения нет. Необходимо прекратить симплекс преобразование.
- Элемент стоящий на пересечении разрешающего столбца и разрешающей строки называется разрешающим элементом:
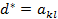
- Переходим к новой симплекс таблице
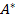 по следующим правилам:
по следующим правилам: - Меняем местами СП и БП соответствующие разрешающему элементу.
- На месте разрешающего элемента в новой таблице стоит величина ему обратная:

- Все элементы разрешающей строки делятся на разрешающее число, включая элемент последнего столбца:

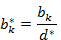
- Все элементы разрешающего столбца делятся на разрешающее число, включая элемент последней строки, с обратным знаком:
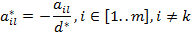

- Все остальные элементы матрицы
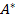 вычисляются по формулам:
вычисляются по формулам:
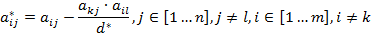
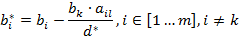
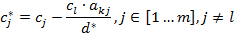
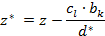
- Если все элементы в Z строке
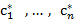 симплекс таблицы
симплекс таблицы 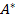 неотрицательны, то достигнуто оптимальное решение, которое равно
неотрицательны, то достигнуто оптимальное решение, которое равно  .
. - Если в Z строке
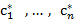 симплекс таблицы
симплекс таблицы 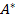 найдется хотя бы один отрицательный элемент, то необходимо выполнить еще одно симплекс преобразование к симплекс таблице
найдется хотя бы один отрицательный элемент, то необходимо выполнить еще одно симплекс преобразование к симплекс таблице 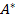 , согласно п.1-6 приведенного выше алгоритма.
, согласно п.1-6 приведенного выше алгоритма.

 и целевую функцию
и целевую функцию  , для которой необходимо определить максимум для заданной системы неравенств. Переменные
, для которой необходимо определить максимум для заданной системы неравенств. Переменные 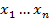 - Свободные Переменные (СП).
- Свободные Переменные (СП). добавляют некоторую неотрицательную величину
добавляют некоторую неотрицательную величину 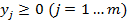 . Переменные
. Переменные  - Базисные Переменные (БП).
- Базисные Переменные (БП).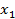
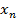
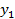
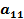








 .
. .
.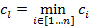
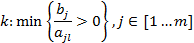
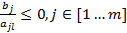 , значит, целевая функция Z неограниченно возрастает и решения нет. Необходимо прекратить симплекс преобразование.
, значит, целевая функция Z неограниченно возрастает и решения нет. Необходимо прекратить симплекс преобразование.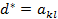
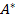 по следующим правилам:
по следующим правилам: 

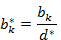
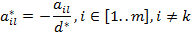

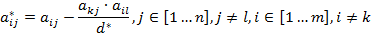
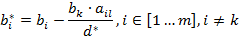
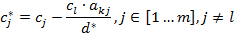
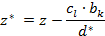
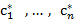 симплекс таблицы
симплекс таблицы  .
.


