Алгоритм 2 Симплекс преобразования на основе укороченных симплекс таблиц
Рассмотрим симплекс-метод для решения задачи Линейного программирования в случае, если существует
Изначально имеем систему неравенств
Тогда укороченная симплекс таблица примет вид:
1. Выбрать строку с наименьшим отрицательным свободным членом в B-столбце
2. Рассмотреть элементы s-ой строки. a. Если b. Если 3. Выбирается разрешающая строка k, которая соответствует наименьшему положительному из отношений элементов правой части уравнений на соответствующие элементы разрешающего столбца:
4. Тогда элемент, стоящий на пересечении разрешающего столбца и разрешающей строки называется разрешающим элементом Замечание: В случае, когда
5. Далее выполняем все п.4 “Алгоритм 1 Симплекс преобразования на основе укороченных симплекс таблиц”. 6. Если в результате симплексного преобразования в столбце свободных членов B все еще есть отрицательные элементы, то необходимо применять п. 1-5 “Алгоритм 2 Симплекс преобразования на основе укороченных симплекс таблиц” до тех пор пока все элементы столбца свободных членов не будут положительными 7. Если в результате симплексного преобразования в столбце свободных членов B нет отрицательных элементов, тогда перейти к применению “Алгоритма 1 Симплекс преобразования на основе укороченных симплекс таблиц” (п.1-6)
|

 .
. и целевую функцию
и целевую функцию  , для которой необходимо определить максимум для заданной системы неравенств. Переменные
, для которой необходимо определить максимум для заданной системы неравенств. Переменные  - Свободные Переменные (СП). Данную систему неравенств необходимо привести к виду, где
- Свободные Переменные (СП). Данную систему неравенств необходимо привести к виду, где  . А затем к приведенной системе применить “Алгоритм 1 Симплекс преобразования на основе укороченных симплекс таблиц”
. А затем к приведенной системе применить “Алгоритм 1 Симплекс преобразования на основе укороченных симплекс таблиц”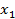
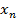
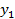
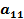









 , следовательно, система несовместна, и задача Линейного программирования не имеет решений
, следовательно, система несовместна, и задача Линейного программирования не имеет решений , то необходимо взять любой
, то необходимо взять любой  и столбец, содержащий данный элемент в качестве разрешающего столбца –
и столбец, содержащий данный элемент в качестве разрешающего столбца –  .
.
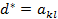 .
.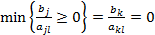 , то элемент
, то элемент  выбирается в качестве разрешающего только в том случае, если
выбирается в качестве разрешающего только в том случае, если  иначе произойдет зацикливание. Если же
иначе произойдет зацикливание. Если же  ,
,  и в строке s кроме элемента
и в строке s кроме элемента  есть еще элемент
есть еще элемент  и при этом
и при этом  , то в качестве разрешающего столбца лучше брать столбец r. И тогда k-я строка уже не будет разрешающей.
, то в качестве разрешающего столбца лучше брать столбец r. И тогда k-я строка уже не будет разрешающей.


