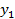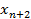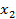Алгоритм 3 Симплекс преобразования на основе укороченных симплекс таблиц для решения двойственной задачи Линейного программирования
Изначально имеем систему неравенств Данная постановка задачи Линейного программирования называется Прямой задачей Линейного программирования. Укороченная симплекс таблица для прямой задачи линейного программирования следующая:
Для любой Прямой задачи Линейного программирования можно построить Двойственную задачу Линейного программирования, которая выглядит так: дана система неравенств При этом решение двойственной задачи Линейного программирования будет решением Прямой задачи Линейного Программирования.
Далее приведем алгоритм симплекс преобразования для решения Двойственной задачи Линейного программирования.
Тогда укороченная симплекс таблица примет вид для двойственной задачи Линейного программирования:
Замечание 1: Все элементы столбца свободных членов C должны быть отрицательны. Замечание 2: Для дальнейшего удобства обозначим элемент в T строке и C столбце
1 Выбирается разрешающую строку k, соответствующую наименьшему отрицательному элементу в С столбце
2. Выбирается разрешающий столбец l, который соответствует наименьшему положительному из отношений элементов T-строки на соответствующие элементы разрешающей строки:
Замечание: Если все отношения
c. Все элементы разрешающей строки делятся на разрешающее число с обратным знаком, включая элемент последнего столбца:
5. Если все элементы в C столбце 6. Если в C столбце 7. Решив Двойственную задачу Линейного Программирования, можно получить решение Прямой задачи Линейного программирования, введя следующее соответствие между СП и БП Прямой и Двойственных задач Линейного программирования:
И при этом Tmin=Zmax=z* Транспонируя симплекс таблицу для двойственной задачи ЛП и вводя переменный xi вместо переменных (±yi), получим оптимальный план решения прямой задачи – необходимо смотреть соответствующие значения в столбце свободных членов.
|

 и целевую функцию
и целевую функцию  , для которой необходимо определит максимум для заданной системы неравенств. Переменные
, для которой необходимо определит максимум для заданной системы неравенств. Переменные 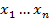 - Свободные Переменные (СП).
- Свободные Переменные (СП).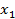
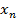

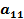


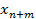





 и целевая функция
и целевая функция  , для которой необходимо определить минимум для заданной системы неравенств.
, для которой необходимо определить минимум для заданной системы неравенств.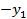

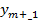

 .
.

 , значит, целевая функция T неограниченно уменьшается, и решения нет. Необходимо прекратить симплекс преобразование.
, значит, целевая функция T неограниченно уменьшается, и решения нет. Необходимо прекратить симплекс преобразование.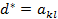
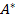 по следующим правилам:
по следующим правилам: 

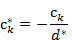
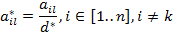
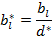




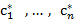 симплекс таблицы
симплекс таблицы  .
.