Задача 5. Используя метод исключения переменных и геометрические построения, найти решение задачи Линейного Программирования:
Используя метод исключения переменных и геометрические построения, найти решение задачи Линейного Программирования:
Решение
1.1 Из третьего ограничения
C учетом условия
Замечание: из третьего ограничения типа равенства можно также выразить любую из переменных
1.2 Подставим выражение для
1.3 Подставим выражение для
1.4 Подставим выражение для
Свободным членом на данном этапе можно пренебречь, тогда перейдем к целевой функции вида:
1.5 Таким образом, после применения метода исключения переменных от исходной задачи перейдем к задаче вида:
Данная задача может быть решена на плоскости графическим методом решения задач линейного программирования.
1.6 Необходимо на плоскости построить прямые, соответствующие заданным неравенствам. Прямая, соответствующая неравенству
Прямая, соответствующая неравенству
Прямая, соответствующая неравенству
1.7 Строим на плоскости прямые, соответствующие данным прямым. 1.8 Определяем ОДЗ (Область допустимых значений) данной системы неравенств. ОДЗ- это многогранник, ограниченный заданной системой неравенств, каждая точка которого удовлетворяет всем неравенствам (условиям).
На данном графике также обозначена область, удовлетворяющая условию Таким образом, ОДЗ, удовлетворяющая всем условиям следующая:
1.9 Строим вектор целевой функции Линия уровня целевой функции
Чтобы определить градиент возрастания целевой функции можно взять две точки выше и ниже линии уровня целевой функции В нашем случае можно взять две точки:
Таким образом целевая функция возрастает вверх (см. рисунок), а вниз соответственно убывает. 1.10 Мысленно передвигая параллельно линию уровня целевой функции вверх, нужно определить крайнюю точку ОДЗ, которую пересекают линии уровня целевой функции.
Для данной ОДЗ целевая функция
Определим координаты точек B и С. Точка В образована пересечением двух прямых
Решив данную систему уравнений, получаем координаты точки B Координаты точки С можно определить из графика: Значение максимума целевой функции будет одинаково на всем участке прямой BC. Определим его, например, в точке С, подставив координаты точки С в
Таким образом, максимум целевой функции достигается на отрезке прямой 1.11 Исходя из графика, целевая функция
Из графика следует, что координаты точки D Определяем минимум целевой функции
Ответ: Максимум целевой функции достигается на отрезке прямой Минимум целевой функции
|

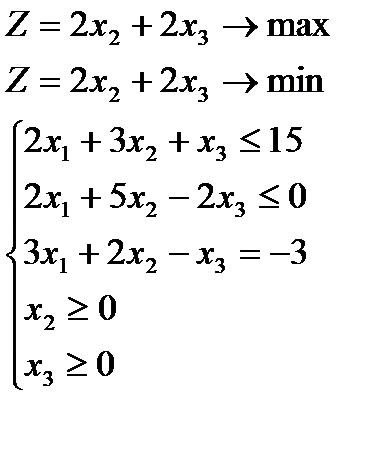
 можно выразить
можно выразить  :
: .
.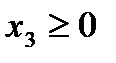 имеем:
имеем:
 или
или 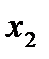 . Это не влияет на конечный результат - значение максимума и минимума целевой функции
. Это не влияет на конечный результат - значение максимума и минимума целевой функции  .
. в первое ограничение
в первое ограничение  :
:
 :
:
 :
:


 , проходит через точки
, проходит через точки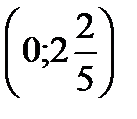 и
и 
 проходит через точки
проходит через точки и
и 
 проходит через точки
проходит через точки и
и 

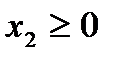 .
.
 . Для этого необходимо построить линию уровня целевой функции, где
. Для этого необходимо построить линию уровня целевой функции, где  , а затем определить в какую сторону целевая функция возрастает.
, а затем определить в какую сторону целевая функция возрастает. проходит через точки
проходит через точки  и
и  .
.
 больше нуля.
больше нуля. и
и  :
:


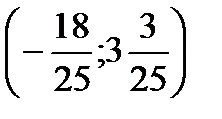 .
. .
.
 , где
, где  , при этом
, при этом 
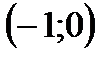 .
.




