Задача 2. Используя геометрические построения, найти решение задачи Линейного Программирования
Используя геометрические построения, найти решение задачи Линейного Программирования
Решение
6. Необходимо на плоскости построить прямые, соответствующие заданным неравенствам. Прямая, соответствующая неравенству
Прямая, соответствующая неравенству
Прямая, соответствующая неравенству
Прямая, соответствующая неравенству
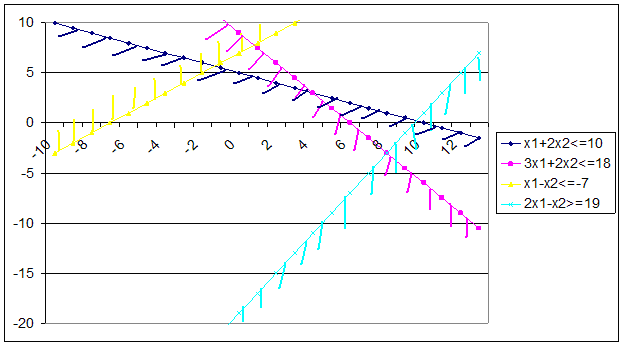
7. Строим на плоскости прямые, соответствующие данным прямым. 8. Определяем ОДЗ (Область допустимых значений) данной системы неравенств. ОДЗ- это многогранник, ограниченный заданной системой неравенств, каждая точка которого удовлетворяет всем неравенствам (условиям):
Для данной системы ограничений не существует ОДЗ – области, которая одновременно удовлетворяет всем условиям одновременно. Поэтому поиск максимума целевой функции в данном случае не имеет смысла.
Ответ: Решения нет, так как ОДЗ для заданной системы ограничений отсутствует.
|


 проходит через точки
проходит через точки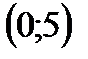 и
и 
 проходит через точки
проходит через точки и
и 
 проходит через точки
проходит через точки и
и 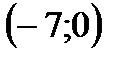
 проходит через точки
проходит через точки и
и