Задача 3. Используя геометрические построения, найти решение задачи Линейного ПрограммированияИспользуя геометрические построения, найти решение задачи Линейного Программирования
Решение 1.4 Необходимо на плоскости построить прямые, соответствующие заданным неравенствам. Прямая, соответствующая неравенству
Прямая, соответствующая неравенству
Прямая, соответствующая неравенству
1.5 Строим на плоскости прямые, соответствующие данным прямым. 1.6 Определяем ОДЗ (Область допустимых значений) данной системы неравенств. ОДЗ- это многогранник, ограниченный заданной системой неравенств, каждая точка которого удовлетворяет всем неравенствам (условиям). В данном случае ОДЗ – полупространство.
На данном графике также обозначены области, удовлетворяющие условиям Таким образом, ОДЗ, удовлетворяющая всем условиям следующая:
1.7 Строим вектор целевой функции Z. Для этого необходимо построить линию уровня целевой функции, где Z=0, а затем определить в какую сторону целевая функция возрастает.
Линия уровня целевой функции
Чтобы определить градиент возрастания целевой функции можно взять две точки выше и ниже линии уровня целевой функции В нашем случае можно взять две точки:
Таким образом целевая функция возрастает вверх (см. рисунок), а вниз соответственно убывает.
1.8 Мысленно передвигая параллельно линию уровня целевой функции вверх, нужно определить крайнюю точку ОДЗ, которую пересекают линии уровня целевой функции.
Для данной ОДЗ крайней точкой, в которой заданная целевая функция достигает минимума, является точка D. Из графика следует, что координаты точки D Подставив координаты точки D в
Ответ:
|
проходит через точки
и 
проходит через точки
и 
проходит через точки
и 
.
проходит через точки 
и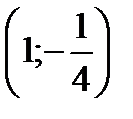 
больше нуля.
и 
:
, получаем значение минимума целевой функции на заданном ОДЗ:
