Задача 4. Для заданной задачи линейного программирования составить двойственную задачу Линейного программирования и решить ее Симплекс методом:
Для заданной задачи линейного программирования составить двойственную задачу Линейного программирования и решить ее Симплекс методом:
Решение 1. Для заданной задачи Линейного программирования Двойственная Задача Линейного программирования выглядит следующим образом:
2. Строим симплекс таблицу для заданной двойственной задачи Линейного программирования
2 Выбираем разрешающую строку k, соответствующую наименьшему отрицательному элементу в С столбце
Следовательно, k =2.
3. Выбираем разрешающий столбец l, который соответствует наименьшему положительному из отношений элементов T-строки на соответствующие элементы разрешающей строки:
Следовательно, l =2.
4. Элемент стоящий на пересечении разрешающего столбца и разрешающей строки называется разрешающим элементом:
c. Все элементы разрешающей строки делятся на разрешающее число с обратным знаком, включая элемент последнего столбца:
Например, вычислим некоторые элементы таблицы:
Полученная СТ2 следующая:
6. В С столбце есть отрицательные элементы (-2), поэтому оптимальное решение не найдено и необходимо сделать еще одно симплекс преобразование. 7. Выбираем разрешающую строку k, соответствующую наименьшему отрицательному элементу в С столбце
Следовательно, k =1.
8. Выбираем разрешающий столбец l, который соответствует наименьшему положительному из отношений элементов T-строки на соответствующие элементы разрешающей строки:
Следовательно, l =3.
9. Элемент стоящий на пересечении разрешающего столбца и разрешающей строки называется разрешающим элементом:
b. На месте разрешающего элемента в новой таблице стоит величина ему обратная:
c. Все элементы разрешающей строки делятся на разрешающее число с обратным знаком, включая элемент последнего столбца:
d. Все элементы разрешающего столбца делятся на разрешающее число, включая элемент последней строки:
e. Все остальные элементы матрицы
Например, вычислим некоторые элементы таблицы:
Полученная СТ3 следующая:
11. Все элементы С столбца положительные, следовательно оптимальное решение найдено. 12. Введем соответствие между СП и БП Прямой и Двойственных задач Линейного программирования
Транспонируя симплекс таблицу для двойственной задачи ЛП и вводя переменный xi вместо переменных (±yi), получаем оптимальный план решения прямой задачи – необходимо смотреть соответствующие значения в столбце свободных членов.
Таким образом, оптимальное решение – максимум целевой функции Z =8 - достигается при
Ответ: Zmax=8 при этом
|

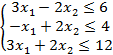
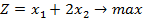
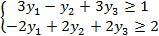
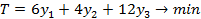
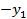


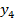
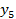
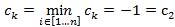
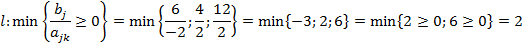
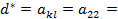 2
2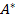 по следующим правилам:
по следующим правилам: 

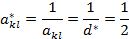


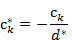
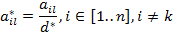
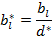





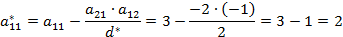



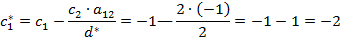


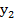

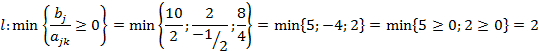
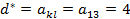
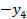
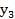
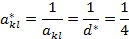











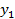
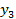

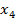
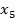
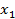
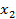
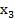
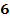
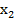
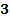
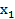
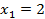 ,
, 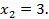 Это полностью совпадает с результатом решения прямой задачи Линейного Программирования (см. Задачу 1)
Это полностью совпадает с результатом решения прямой задачи Линейного Программирования (см. Задачу 1)



