Решение. 1. Проверим, есть ли у данной игры решение в области смешанных стратегий, т.е
1. Проверим, есть ли у данной игры решение в области смешанных стратегий, т.е. есть ли у заданной матрицы седловая точка. a. Найдем нижнюю цену игры
b. Найдем верхнюю цену игры
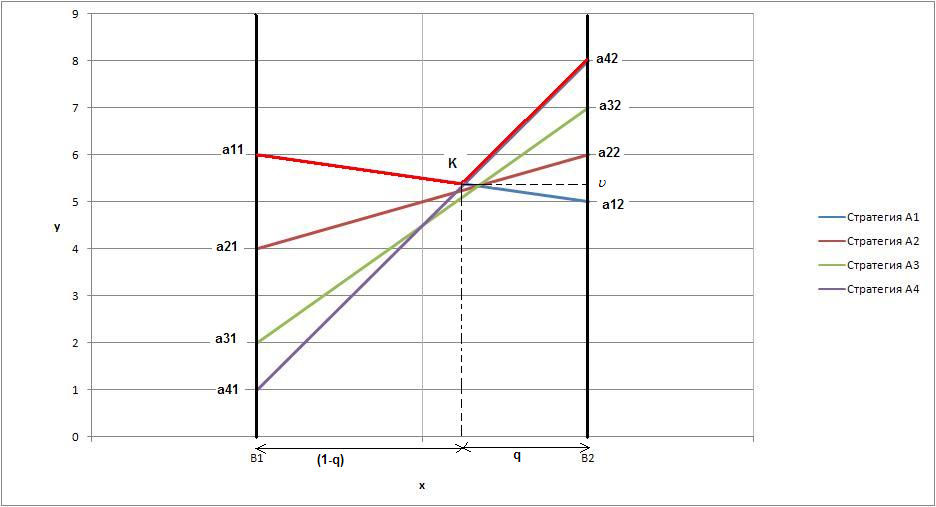
c. Нижняя цена игры не равна верхнее цены игры, следовательно, седловой точки у заданной матрицы выигрышей нет и решения в чистых стратегиях отсутствует. Поэтому решение необходимо искать в области смешанных стратегий. 2. Матрица имеет размерность 4 x 2. В этом случае строим прямые, соответствующие стратегиям игрока 1.
3. Ломанная a11Ka42 соответствует верхней границе выигрыша игрока 1, а отрезок – перпендикуляр из точки K до оси x - цене игры.
Таким образом, полезными стратегиями первого игрока (Полезные стратегии – это те стратегии, который входят в состав оптимальной смешанной стратегии) являются стратегии А1 и А4, так как точка К образована пересечением именно этих стратегий. 4. Тогда можно перейти к матрице А* 2 х 2:
5. Находим оптимальную смешанную стратегию первого игрока, применив формулу (6):
Следовательно, оптимальная смешанная стратегия первого игрока X= 6. Находим цену игры, применив формулу (7):
Проверка: цена игры
Это неравенство выполнено:
7. Находим оптимальную смешанную стратегию второго игрока, используя формулу (9):
Следовательно, оптимальная смешанная стратегия второго игрока Y=
Ответ: Оптимальное решение находится в области смешанных стратегий. Оптимальная стратегия первого игрока X=
|

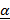 :
:
 :
: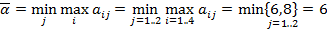


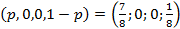 . Стратегии А2 и А3 не входят в оптимальную смешанную стратегию (это видно из рисунка), поэтому частота (вероятность) их использования равна нулю.
. Стратегии А2 и А3 не входят в оптимальную смешанную стратегию (это видно из рисунка), поэтому частота (вероятность) их использования равна нулю.
 должна удовлетворять следующему неравенству:
должна удовлетворять следующему неравенству:

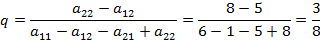
 .
. , оптимальная стратегия второго игрока Y=
, оптимальная стратегия второго игрока Y=  , цена игры
, цена игры 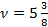 .
.


