Распределение признака. Параметры распределения

Полученные в исследовании эмпирические данные подлежат проверке на распределение их в выборках по отношению к средней (арифметической, медиане или моде).

Распределением признака называется закономерность встречаемости разных его значений. В психологических исследованиях чаще всего ссылаются на нормальное распределение.

Одним из важнейших в математической статистике является понятие нормального распределения. Нормальное распределение – модель варьирования некоторой случайной величины, значения которой определяются множеством одновременно действующих независимых факторов. Число таких факторов велико, а эффект влияния каждого из них в отдельности очень мал. Такой характер взаимовлияний весьма характерен для психических явлений, поэтому исследователь в области психологии чаще всего выявляет нормальное распределение. Однако так бывает не всегда, поэтому в каждом случае форма распределения должна быть проверена. Характер распределения выявляется главным образом с целью определиться в методах математико-статистической обработки данных.

Нормальное распределение характеризуется тем, что крайние значения признака в нем встречаются достаточно редко, а значения, близкие к средней величине - достаточно часто. Нормальным такое распределение называется потому, что оно очень часто встречалось в естественно-научных исследованиях и казалось «нормой» всякого массового случайного проявления признаков. График нормального распределения представляет собой привычную глазу психолога-исследователя так называемую колоколообразную кривую (рис. А).

 

 

Рис. А. Кривая нормального распределения

 

Параметры распределения – это его числовые характеристики, указывающие, где «в среднем» располагаются значения признака, насколько эти значения изменчивы и наблюдается ли преимущественное появление определенных значений признака. Наиболее практически важными параметрами являются математическое ожидание, дисперсия, показатели асимметрии и эксцесса.

В реальных психологических исследованиях мы оперируем не параметрами, а их приближенными значениями, так называемыми оценками параметров. Это объясняется ограниченностью обследованных выборок. Чем больше выборка, тем ближе может быть оценка параметра к его истинному значению. В дальнейшем, говоря о параметрах, мы будем иметь в виду их оценки.

Для определения способов математико-статистической обработки прежде всего необходимо оценить характер распределения данных по всем используемым параметрам (признакам). Для параметров (признаков), имеющих нормальное распределение или близкое к нормальному, можно использовать методы параметрической статистики, которые во многих случаях являются более мощными, чем методы непараметрической статистики. Достоинством последних является то, что они позволяют проверять статистические гипотезы независимо от формы распределения.

Если характер распределения показателей психологического признака является нормальным или близким к нормальной форме распределения признака, описываемой кривой Гаусса, то мы можем использовать параметрические методы математической статистики как наиболее простые, надежные и достоверные: сравнительный анализ, расчет достоверности отличий признака между выборками по f-критерию Стьюдента, F-критерию Фишера, коэффициент корреляции Пирсона и др.

Если кривая распределения показателей психологического признака далека от нормальной, то мы вынуждены будем использовать методы непараметрической статистики: расчет достоверности отличий по критерию Q Розенбаума (для малых выборок), по критерию U Манна – Уитни, коэффициент ранговой корреляции Спирмена, факторный, многофакторный, кластерный и другие методы анализа.

Помимо этого, по характеру распределения можно составить общее представление об общей характеристике выборки испытуемых по данному признаку и тому, насколько данная методика соответствует (т. е. «работает», валидна) данной выборке.

Для нормального распределения характерно следующее:

а) все три средние совпадают;

б) кривая распределения частот и значений совершенно симметрична по отношению к средней, т. е. слева и справа от нее лежит 50% вариантов; в интервале от М -lo до М +1о находится 68, 26% всех вариантов; в интервале от М -2о до М +2о лежит 95, 44% вариантов.

В психологии существует ряд шкал, основанных на нормальном распределении и имеющих разные значения М и σ. Распределения различных измеренных в эксперименте признаков имеют разные величины М и σ. Переводя полученные первичные оценки разных признаков к распределению с одними и теми же М и σ, мы получаем больше возможностей для оценки и сопоставления их варьирования. Сделать это нам позволяет использование нормированного отклонения. Нормированное отклонение показывает, на сколько сигм отклоняется та или иная варианта от среднего уровня варьирующего признака (средней арифметической), и выражается формулой:

 

 

где Хi – значение признака (в «сырых» баллах);

М – средняя арифметическая признака;

σ – стандартное отклонение.

С помощью нормированного отклонения можно оценить любое полученное значение по отношению к группе в целом, взвесить его отклонение и одновременно освободиться от именованных величин. Для того чтобы избавиться от отрицательных чисел, к полученной величине t обычно прибавляют какую-либо константу.

С учетом этих соображений весьма удобна шкала Г-баллов. Для этой шкалы принято нормальное распределение, имеющее М = 0, σ = 10.

 

 

Рис. Б. Расчет нормального распространения по шкале Г-баллов

 

Для пересчета берется константа, равная 50. Формула преобразования сырых оценок в Г-баллы следующая:

 

 

где Хi – значение признака (в «сырых» баллах);

М – средняя арифметическая признака;

σ – стандартное отклонение.

Для облегчения и алгоритмизации практической работы психолога существуют специальные таблицы перевода «сырых» баллов, например, базовых шкал теста СМИЛ (адаптированный вариант теста MMPI, разработан Л. Н. Собчик), теста МЛО «Адаптивность» в стандартные Г-баллы.

Наиболее широкое распространение получил способ приведения нормированных оценок к виду, удобному для практического применения, предложенный Р. Б. Кэттеллом (1970, 1973), который представляет перевод исходных тестовых оценок в 10-балльную равноинтервальную шкалу. Это достигается путем разбиения оси тестовых оценок на 10 интервалов, соответствующих долям стандартного отклонения.

 

 

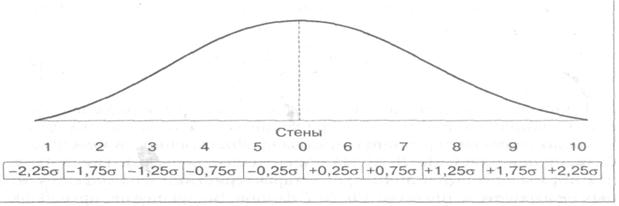
Рис. В. Нормальное распространение для равноинтервальных шкал

 

При этом среднее арифметическое по группе принимается за среднюю точку и ей присваивается значение, равное 5, 5 балла по стандартной 10-балльной шкале. Всякая оценка в интервале (М + 0, 25 σ) переводятся в 6 баллов, а оценка в (М – 0, 25 σ) дает стандартный балл, равный 5, 0. Любое дальнейшее увеличение или уменьшение тестовой оценки на 0, 5 σ увеличивает или уменьшает стандартную оценку на 1 балл.

Таким образом, для создания стеновой шкалы и вычисления ее пограничных значений «сырых» баллов можно использовать следующую таблицу (при условии нормального распределения признака или близкого к нормальному).

1 стен = М – 2, 25 σ

2 стен = М – 1, 75 σ

3 стен = М – 1, 25 σ

4 стен = М – 0, 75 σ

5 стен = М – 0, 25 σ

6 стен = М + 0, 25 σ

7 стен = М + 0, 75 σ

8 стен = М + 1, 25 σ

9 стен = М + 1, 75 σ 10 стен = М + 2, 25 σ

 

Перевод отдельных «сырых» баллов в стены может выполняться и без создания стеновой шкалы, а непосредственно по общей формуле:

 

где Хi – значение признака (в «сырых» баллах);

М – средняя арифметическая признака;

А – заданное стандартное отклонение;

С – заданное среднее значение;

σ – стандартное отклонение значений признака.

Таким образом, практический смысл процедуры нормирования состоит, например, в том, что выражение «сырых» значений шкал в Г-баллах позволяет сравнивать шкалы профиля личности между собой (для опросников СМИЛ, МЛО «Адаптивность» и др.). Так, в пределах нормы считаются личностные характеристики, показатели которых не выходят за пределы 40 –70 Г-баллов. Все значения, превышающие эти границы, рассматриваются как акцентуации характера той или иной степени выраженности (в отдельных случаях – до уровня патологических проявлений).