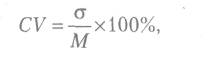Первичная обработка эмпирических данных
Каждое изучаемое психическое явление имеет множество признаков, по которым мы можем узнать его, отличить от других явлений. Психические явления, непосредственно наблюдаемые и не наблюдаемые, также имеют признаки и поддаются объективным и (или) субъективным оценкам (т. е. могут быть принципиально измеряемы и регистрируемы). Психологическое исследование непременно связано с выделением признаков (существенных для предмета исследования), регистрацией их наличия или отсутствия, определенной степени выраженности. Чтобы зафиксировать проявления того или иного признака, исследователь использует те или иные показатели выраженности признака. Показатель – то, по чему можно судить о развитии и ходе чего-нибудь (т. е. это конкретное числовое или качественное выражение какого-либо признака). В качестве синонима термина «показатель» нередко используют заимствованный из технических наук термин «параметр» (или варианта – показатель отдельного признака в математической статистике), параметр – величина (качественная или количественная), характеризующая какую-либо выраженность характеристики, свойства, качества исследуемого психологического признака. К числу основных понятий планирования эксперимента и обработки данных относится также понятие «переменная». В математике под переменной называют величину, которая может по условиям задачи принимать разные значения. В математической статистике понятия «переменная», «параметр», «варианта» (отдельное значение признака) используются зачастую как синонимы, хотя такое понимание не совсем корректно, но, не вдаваясь в детали, вполне возможно в практическом использовании. Например, исследуется время реакции на движущийся объект. В данном случае исследуемым признаком будет выступать сенсомоторная реакция, а показателями, вариантами (отдельными значениями) будет выступать время реакции, измеренное с помощью секундомера. В ходе опыта, эксперимента, измеряя тот или иной показатель или фиксируя в наблюдении проявление некоторого признака, психолог получает конкретное значение показателя у отдельного испытуемого. Совокупность значений всех показателей (вариант – показателей отдельного признака) заносится в протокол данного испытуемого. Совокупность всех собранных в ходе эмпирического исследования данных образует массив данных. Таким образом, в процессе математико-статистической обработки данных мы будем использовать следующие термины: • «признак» – обозначение исследуемого психического явления, то, что выражает природу явления их сходство и различия (например, ЛТ – личностная тревожность; РТ – реактивная тревожность; IQ – общий уровень интеллектуального развития и т. д.); • «параметр» и «переменная» нередко употребляются как синонимы, они указывают, что изменяется. Важно отличать от них понятие «значение» (или, в математической статистике, варианта – отдельное значение признака). Каждое значение (варианта) – это эмпирически выявленная, вполне определенная числовая величина того или иного признака у конкретного испытуемого (измеренная в шкале наименований, рангов или интервальной), представленная (желательно) в десятичном числовом выражении: 1; 3; 5; 10; 100; 0, 1; 0, 54; 0, 78; 0, 001 и т. д. Для методов контент-анализа и проективных методик понятие «параметр» и «переменная» значительно усложняются в связи с их качественной характеристикой, представленностью и интерпретацией. Важнейшими первичными статистиками являются: средние значения (М и Me), среднее квадратичное или стандартное отклонение, обозначаемое греческой буквой σ (сигма) и коэффициент вариаций V. Среднее арифметическое признака (М или Х) – это величина, сумма отрицательных и положительных отклонений от которой равна нулю. Чтобы ее подсчитать, надо суммировать все значения ряда и разделить сумму на количество суммированных значений. Среднее квадратичное отклонение (σ) – мера отклонения каждого варианта от средней арифметической, мера разнообразия входящих в группу объектов; она показывает, насколько в среднем отклоняется каждая варианта (конкретное значение оцениваемого параметра) от средней арифметической. Чем сильнее разбросаны варианты относительно средней, тем большим оказывается и среднее квадратичное отклонение. Разброс значений характеризует и размах – разность между наибольшим и наименьшим значением в ряду. Однако сигма полнее характеризует разброс значений относительно средней арифметической. Определяется по формуле:
где Xi – каждое наблюдаемое значение признака; Хар – среднее арифметическое значение признака; п – количество наблюдений. Коэффициент вариации получается в результате деления сигмы на среднее арифметическое, умноженное на 100. Обозначается CV:
где σ – стандартное отклонение; CV – коэффициент вариации; М – среднее арифметическое. В научных исследованиях по части (отдельной выборке) никогда не удается полностью охарактеризовать целое (генеральную совокупность, популяцию, всегда остается вероятность того, что оценка генеральной совокупности на основе выборочных данных недостаточно точна, имеет некоторую большую или меньшую ошибку. Такие ошибки, представляющие собой ошибки обобщения, экстраполяции, связанные с перенесением результатов, полученных при изучении выборки, на всю генеральную совокупность, называются ошибками репрезентативности. Репрезентативность – степень соответствия выборочных показателей генеральным параметрам. Статистические ошибки репрезентативности показывают, в каких пределах могут отклоняться от параметров генеральной совокупности (от математического ожидания или истинных значений) наши частные определения, полученные на основе конкретных выборок. Очевидно, величина ошибки тем больше, чем больше варьирование признака и чем меньше выборка. Это и отражено в формулах для вычисления статистических ошибок, характеризующих варьирование выборочных показателей вокруг их генеральных параметров. Поэтому в число первичных статистик обязательно входит статистическая ошибка средней арифметической. Формула для ее вычисления такова:
где mм – ошибка средней арифметической; σ – сигма, стандартное отклонение; п – число значений признака.
Первичные статистики необходимы для интерпретации эмпирических данных: · на основе полученных значений М или Me можно, например, предвидеть наиболее вероятные результаты аналогичного исследования другой выборки; · на основе среднего квадратичного отклонения (σ) и коэффициента вариации (V) можно оценить точность проведенных измерений; · та или другая из названных мер необходима для проверки статистической значимости различий (t-критерий Стьюдента) между результатами исследования двух разных выборок, а также для вычисления коэффициентов корреляции между переменными. Полученные при сборе данных «сырые» (первичные) оценки выполнения экспериментальных заданий далеко не всегда удобно использовать в дальнейшей работе. Особенно когда возникает необходимость сравнить показатели испытуемого, полученные по разным методикам, или отнести их к какой-либо группе («успешных», «неуспешных», «норме» – в целях профотбора). Поэтому данные «сырые» оценки тем или иным способом преобразуют. Наиболее частыми преобразованиями является стандартизация тестовых шкал. Тестовые шкалы разрабатываются для того, чтобы оценить индивидуальный результат тестирования путем сопоставления его с тестовыми нормами, полученными на выборке стандартизации. Выборка стандартизации специально формируется для разработки тестовой шкалы – она должна быть репрезентативна генеральной совокупности, для которой планируется применять данный тест, методику. Впоследствии при тестировании предполагается, что и испытуемый, и выборка стандартизации принадлежат одной и той же генеральной совокупности. Наиболее частыми преобразованиями являются центрирование и нормирование среднеквадратическими отклонениями: · Под центрированием понимается линейная трансформация величин признака, при которой средняя величина распределения определенного признака становится равной нулю. Направление шкалы и ее единицы остаются при этом неизменными. · Суть нормирования состоит в переходе к другому масштабу – стандартизированным (стандартным) единицам измерения. При стандартизации результатов тестовых испытаний чаще всего используется показатель среднеквадратических отклонений. Стандартизация осуществляется при условии нормального распределения тестовых оценок или близком к нему по виду.
|