Сущность корреляционного анализа
Первоначальное значение термина «корреляция» – взаимная связь. Когда говорят о корреляции, используют термины «корреляционная связь» и «корреляционная зависимость». Корреляционная связь – это согласованные изменения двух признаков, когда изменчивость одного признака находится в некотором соответствии с изменчивостью другого. В корреляционных связях каждому значению одного признака может соответствовать определенное распределение значений другого признака, но не определенное его значение. Корреляционная зависимость – изменения, которые вносят значения одного признака в вероятность появления разных значений другого признака. Зависимость подразумевает влияние, связь – любые согласованные изменения, которые могут объясняться сотнями причин. Корреляционные связи не могут рассматриваться как свидетельство причинно-следственной связи, они свидетельствуют лишь о том, что изменениям одного признака, как правило, сопутствуют определенные изменения другого, но находится ли причина изменений в одном из признаков или она оказывается за пределами исследуемой пары признаков, нам неизвестно. Говорить в строгом смысле о зависимости мы можем только в тех случаях, когда сами оказываем какое-то контролируемое воздействие на испытуемых или так организуем исследование, что оказывается возможным точно определить интенсивность не зависящих от нас воздействий. Независимая переменная – воздействие, которое мы можем качественно определить или даже измерить. Зависимая переменная – признак, который мы измеряем и который, по нашему предположению, может изменяться под влиянием независимой переменной. Зависимость переменных – согласованные изменения независимой и зависимой переменной. Однако, учитывая, что число градаций, или уровней, зависимой переменной обычно невелико, целесообразнее применять в такого рода исследованиях не корреляционный метод, а методы выявления тенденций изменения признака при изменении условий, например, метод дисперсионного анализа. Если в исследование включены независимые переменные, которые мы можем по крайней мере учитывать, например, возраст, то можно считать выявляемые между возрастом и психологическими признаками корреляционные связи корреляционными зависимостями. В большинстве случаев нам трудно определить, что в рассматриваемой паре признаков является независимой, а что – зависимой переменной. Учитывая, что термин «зависимость» явно или неявно подразумевает влияние, лучше пользоваться более нейтральным термином корреляционная «связь». Корреляционные связи различаются по форме, направлению и степени (силе). По форме корреляционная связь может быть прямолинейной или криволинейной. Прямолинейной может быть, например, связь между количеством тренировок на тренажере и количеством правильно решаемых задач в контрольной сессии. Криволинейной может быть, например, связь между уровнем мотивации и эффективностью выполнения задачи. При повышении мотивации эффективность выполнения задачи сначала возрастает, затем достигается оптимальный уровень мотивации, которому соответствует максимальная эффективность выполнения задачи; дальнейшему повышению мотивации сопутствует уже снижение эффективности. По направлению корреляционная связь может быть положительной («прямой») и отрицательной («обратной»). Положительная прямолинейная корреляция – согласованные изменения, когда более высоким значениям одного признака соответствуют более высокие значения другого, а более низким значениям одного признака – низкие значения другого. Отрицательная прямолинейная корреляция – согласованные изменения, когда более высоким значениям одного признака соответствуют более низкие значения другого, а более низким значениям одного признака – высокие значения другого. При положительной корреляции коэффициент корреляции имеет положительный знак, например: г = +0, 207, при отрицательной корреляции – отрицательный знак, например: г = – 0, 207. Степень, сила или теснота корреляционной связи определяется по величине коэффициента корреляции. Сила связи не зависит от ее направленности и определяется по абсолютному значению коэффициента корреляции. Максимальное возможное абсолютное значение коэффициента корреляции г = 1, 0; минимальное г = 0. Нулевой называется корреляция при отсутствии связи переменных. Используется две системы классификации корреляционных связей по их силе: общая и частная. · Общая классификация корреляционных связей (по Ивантер Э. В., Коросову А. В., 1992): 1) сильная, или тесная при коэффициенте корреляции г > 0, 70; 2) средняя 0, 50 < г < 0, 69; 3) умеренная 0, 30 < г < 0, 49; 4) слабая 0, 20 < г < 0, 29; 5) очень слабая г < 0, 19. · Частная классификация корреляционных связей: 1) высокая значимая корреляция при г, соответствующем уровню статистической значимости р< 0, 01; 2) значимая корреляция при г, соответствующем уровню статистической значимости р< 0, 05; 3) тенденция достоверной связи при г, соответствующем уровню статистической значимости р< 0, 10; 4) незначимая корреляция при г, не достигающем уровня статистической значимости. Две эти классификации не совпадают. Первая ориентирована только на величину коэффициента корреляции, а вторая определяет, какого уровня значимости достигает данная величина коэффициента корреляции при данном объеме выборки. Чем больше объем выборки, тем меньшей величины коэффициента корреляции оказывается достаточно, чтобы корреляция была признана достоверной. В результате при малом объеме выборки может оказаться так, что сильная корреляция окажется недостоверной. В то же время при больших объемах выборки даже слабая корреляция может оказаться достоверной. Обычно принято ориентироваться на вторую классификацию, поскольку она учитывает объем выборки. Вместе с тем необходимо помнить, что сильная, или высокая корреляция – это корреляция с коэффициентом г > 0, 70, а не просто корреляция высокого уровня значимости. В качестве мер корреляции используются: 1) эмпирические меры тесноты связи, многие из которых были получены еще до открытия метода корреляции, а именно: · коэффициент ассоциации, или тетрахорический показатель связи; · коэффициенты взаимной сопряженности Пирсона и Чупрова; · коэффициент Фехнера; · коэффициент корреляции рангов; 2) линейный коэффициент корреляции г; 3) корреляционное отношение п; 4) множественные коэффициенты корреляции и др. 2. Коэффициенты взаимной сопряженности Чупрова – К и Пирсона – С Если мы имеем дело с переменными, измеренными в шкале наименований (измерительная шкала, предназначенная для классификации объектов и предметов: 1 – холерик, 2 – флегматик, 3 – сангвиник, 4 – меланхолик), то пользуемся понятием сопряженности. В этом случае для количественной характеристики многомерных связей используются информационные коэффициенты. К ним относятся в том числе и коэффициенты взаимной сопряженности Чупрова К и Пирсона С. Когда каждый из качественных признаков состоит более чем из двух групп, то для определения тесноты связи используется коэффициент взаимной сопряженности Чупрова К, его иногда называют коэффициентом среднеквадратической сопряженности Чупрова К:
Коэффициент Пирсона С применяется в тех случаях, когда совпадают числа строк и столбцов и нет необходимости подсчитывать частоту появления различных значений переменных X и У, и вычисляется по формуле:
где φ – определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки. Отметим, что оба коэффициента изменяются только от 0 до 1 и измеряют тесноту сопряженности, не указывая ее направления, о котором легко судить по форме совместного распределения вероятностей (частот) событий. Чем ближе К и С к 1, тем связь теснее.
|



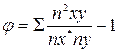 показатель взаимной сопряженности;
показатель взаимной сопряженности;


