Переход от одной системы координат в другую. Якобиан перехода
Рассмотрим переход из системы
Рассмотрим переход к полярным координатам в двойном интеграле:
Тогда формула перехода к полярным координатам имеет вид:
Пример 195 Найти якобиан перехода из системы Решение Пример 196 Перейти к полярным координатам в двойном интеграле, если Решение Запишем уравнение этой кривой в полярных координатах:
Пример 197 Перейти к полярным координатам в двойном интеграле, если Решение Радиус-вектор обходит прямую
Пример 198 Вычислить двойной интеграл
Решение Область
|
в систему 
с помощью формул: 
. Якобиан (коэффициент) перехода вычисляется по формуле
.
, 
,
.
.
, 
.
.
.
.
.
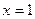, поэтому запишем уравнение этой прямой в полярных координатах:
.
.
, если 
.
является кольцом между окружностями, уравнения которых в полярных координатах имеет вид: 
.
.
