Признак Даламбера: 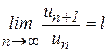 , если
, если  , то ряд сходится; если
, то ряд сходится; если  , то ряд расходится.
, то ряд расходится.
Радикальный признак Коши:  , если
, если  , то ряд сходится; если
, то ряд сходится; если  , то ряд расходится.
, то ряд расходится.
Интегральный признак Коши: если  сходится, то ряд тоже сходится, если
сходится, то ряд тоже сходится, если 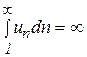 расходится, то ряд тоже расходится.
расходится, то ряд тоже расходится.
Признак сравнения: Если даны два ряда  ,
,  и выполняется условие
и выполняется условие  , то из сходимости второго ряда следует сходимость первого ряда, а из расходимости первого ряда следует расходимость второго ряда.
, то из сходимости второго ряда следует сходимость первого ряда, а из расходимости первого ряда следует расходимость второго ряда.
Пример 212 Исследовать на сходимость ряд  .
.
Решение Воспользуемся радикальным признаком Коши
 , ряд сходится.
, ряд сходится.
Пример 213 Исследовать на сходимость ряд  .
.
Решение По признаку Даламбера
 , ряд сходится.
, ряд сходится.
Пример 214 Сходимость ряда  проверим по интегральному признаку Коши:
проверим по интегральному признаку Коши:  , интеграл равен конечному числу, т.е. сходится, значит ряд сходится.
, интеграл равен конечному числу, т.е. сходится, значит ряд сходится.
Пример 215 В силу интегрального признака Коши ряд  расходится,
расходится,  .
.
Пример 216 Ряд  называется гармоническим. Он расходится, так как
называется гармоническим. Он расходится, так как  .
.

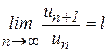 , если
, если  , то ряд сходится; если
, то ряд сходится; если  , то ряд расходится.
, то ряд расходится. , если
, если  сходится, то ряд тоже сходится, если
сходится, то ряд тоже сходится, если 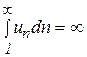 расходится, то ряд тоже расходится.
расходится, то ряд тоже расходится. ,
,  и выполняется условие
и выполняется условие  , то из сходимости второго ряда следует сходимость первого ряда, а из расходимости первого ряда следует расходимость второго ряда.
, то из сходимости второго ряда следует сходимость первого ряда, а из расходимости первого ряда следует расходимость второго ряда. .
. , ряд сходится.
, ряд сходится. .
. , ряд сходится.
, ряд сходится. проверим по интегральному признаку Коши:
проверим по интегральному признаку Коши:  , интеграл равен конечному числу, т.е. сходится, значит ряд сходится.
, интеграл равен конечному числу, т.е. сходится, значит ряд сходится. расходится,
расходится,  .
. называется гармоническим. Он расходится, так как
называется гармоническим. Он расходится, так как  .
.


