Если задана функция 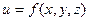 , то ее можно принять как скалярное поле, зависящее от координат точек либо просто скалярная функция скалярных аргументов. Скорость изменения этой функции по направлению некоторого вектора
, то ее можно принять как скалярное поле, зависящее от координат точек либо просто скалярная функция скалярных аргументов. Скорость изменения этой функции по направлению некоторого вектора 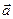 определяется по формуле (производная по направлению):
определяется по формуле (производная по направлению):
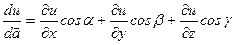
где 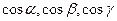 - направляющие косинусы вектора
- направляющие косинусы вектора 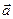 .
.
Пример 173 Найти производную функции  в точке
в точке 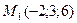 по направлению вектора
по направлению вектора 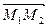 , если
, если  .
.
Решение  ,
, 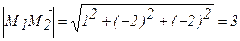 ,
,
 ,
, 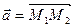
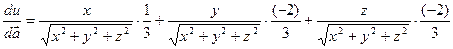
 .
.
Пример 174 Вычислить производную функции 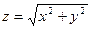 в точке
в точке 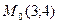 по направлению вектора
по направлению вектора 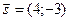 .
.
Решение 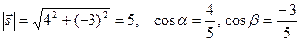
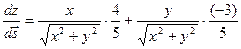
 .
.
Градиентом функции  (поля) называется вектор
(поля) называется вектор
 .
.
Пример 175 Найти  в точке М0(1; 1; 1), если
в точке М0(1; 1; 1), если  .
.
Решение 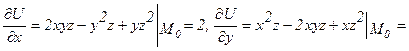
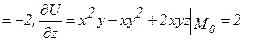 ,
, 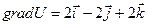 или
или
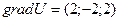 .
.
Дифференциальные уравнения
Уравнения первого порядка
Таблица 1
|
Название
|
Тип
|
Метод распознавания
|
|
C разделяющимися переменными
|

|
Переменные разделяются алгебраическим путем
|
|
Однородное уравнение
|

|
 однородные функции одной степени. однородные функции одной степени.
|
|
Линейное уравнение 1-го порядка
|
 или или
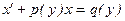
|
По виду
|
|
Уравнение Бернулли
|

|
По виду
|
| В полных дифференциалах
|

| 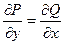
|
Пример 176 Определить тип уравнений
а) 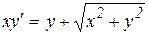 − однородное, так как
− однородное, так как
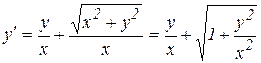
является функцией от отношения переменных;
б) 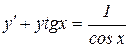 − линейное уравнение 1-го порядка;
− линейное уравнение 1-го порядка;
в)  − с разделяющимися переменными, так как
− с разделяющимися переменными, так как
 ;
;
г)  - уравнение Бернулли. Запишем по другому это уравнение
- уравнение Бернулли. Запишем по другому это уравнение  ;
;
д) 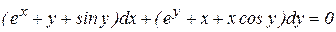 - в полных дифференциалах, так как
- в полных дифференциалах, так как
 .
.
Пример 177 Найти общее решение (общий интеграл) дифференциального уравнения 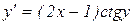 .
.
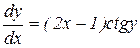 ,
,  ,
,
 ,
, 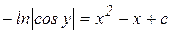 .
.
Пример 178 Найти общее решение дифференциального уравнения  .
.
Решение 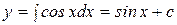 .
.
Пример179 Найти общий интеграл дифференциального уравнения 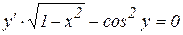 .
.

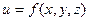 , то ее можно принять как скалярное поле, зависящее от координат точек либо просто скалярная функция скалярных аргументов. Скорость изменения этой функции по направлению некоторого вектора
, то ее можно принять как скалярное поле, зависящее от координат точек либо просто скалярная функция скалярных аргументов. Скорость изменения этой функции по направлению некоторого вектора 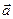 определяется по формуле (производная по направлению):
определяется по формуле (производная по направлению):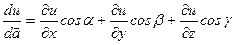
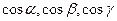 - направляющие косинусы вектора
- направляющие косинусы вектора  в точке
в точке 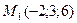 по направлению вектора
по направлению вектора 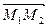 , если
, если  .
. ,
, 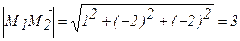 ,
, ,
, 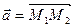
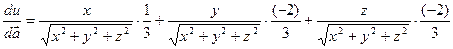
 .
.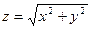 в точке
в точке 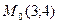 по направлению вектора
по направлению вектора 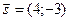 .
.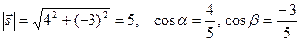
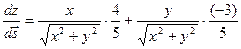
 .
. (поля) называется вектор
(поля) называется вектор .
. в точке М0(1; 1; 1), если
в точке М0(1; 1; 1), если  .
.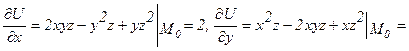
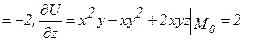 ,
, 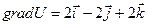 или
или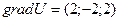 .
.

 однородные функции одной степени.
однородные функции одной степени.
 или
или
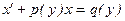


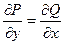
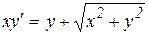 − однородное, так как
− однородное, так как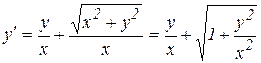
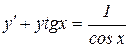 − линейное уравнение 1-го порядка;
− линейное уравнение 1-го порядка; − с разделяющимися переменными, так как
− с разделяющимися переменными, так как ;
; - уравнение Бернулли. Запишем по другому это уравнение
- уравнение Бернулли. Запишем по другому это уравнение  ;
;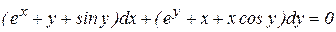 - в полных дифференциалах, так как
- в полных дифференциалах, так как .
.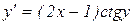 .
.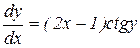 ,
,  ,
, ,
, 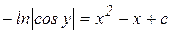 .
. .
.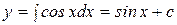 .
.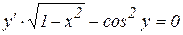 .
.


