Область определения функции
Область определения для функции двух переменных можно изобразить как множество точек плоскости Оху, соответствующих данной функции. Для этого выделяем особенность данной функции в виде неравенства и решаем это неравенство геометрическим путем.
Пример 152 Найти область определения функции Решение Так как функция содержит радикал, то
Пример 153 Найти область определения функции Решение Аналогично предыдущему примеру,
Пример 154 Найти область определения функции Решение Областью определения данной функции является множество точек, удовлетворяющих неравенству
|
.
, 
. Данному неравенству соответствует левая сторона параболы вокруг оси Ох, включая точки параболы. Вершина параболы находится в точке (2; 0).
, 
. Областью определения является внешняя часть круга с центром в точке (0; 0) радиусом равным 3, включая точки окружности.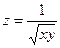
.
или 
, 
. Это точки первого и третьего квадрантов, не включая точек, лежащих на координатных осях.
