Умножение комплексных чисел в тригонометрической форме
Модули умножаются, а аргументы складываются.
Пример 235
Деление
Модули делятся, а аргументы вычитаются.
Пример 236
Возведение в степень
Пример 237 Извлечение корня
где
Пример 238
Решение
15.9 Показательнаяформа комплексного числа Воспользуемся формулами Эйлера:
можно показать, что
Тогда из тригонометрической формы можно перейти в показательную форму.
показательная форма комплексного числа. Все действия выполняются после перехода в тригонометрическую форму.
Операционное исчисление
Функция Функцию
Таблица некоторых изображений Таблица 4
Пример 239 Найти изображение функции:
(воспользовались 2-м и 3-м пунктами таблицы).
Пример 240 Найти оригинал изображения:
Решение
Пример 241 Найти оригинал изображения: Решение Преобразуем
(8-й пункт таблицы).
Пример 242 Найти оригинал изображения Решение
(9, 8 пункты таблицы).
Пример 243 Найти изображение функции
Решение
(Использованы пункты 5, 7, 1 таблицы).
|
.
.
.
.
.
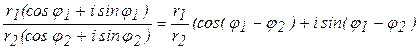− й степени:
,
.
.
.
.
.
.
.
, 
.
.
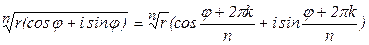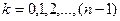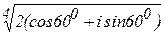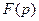называется лапласовым изображением, или 
- изображением, или просто изображениемфункции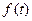 
.
или 
или 
.
.
.
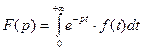
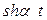
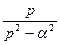
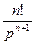
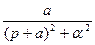
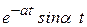
(2, 3 пункты таблицы).
.
:
.
.
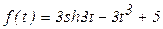