Test questions
1. The method to determine the basic mechanical characteristics of materials. 2. What values characterize the material strength and ductility? 3. What distinctive points and regions does the low carbon steel tension diagram have? 4. What are: the proportional limit, yield strength, ultimate strength? 5. Which diagrams of stresses do we call conditional and which the true ones? 6. The units to measure force, stress, deformation. Literature
1.Wiliam A.Nash. Theory and problems of strength of materials. Third edition. - New York: Schaum s outline series, 1994, - 424 p. 2. Feodosiev V.l. Strength of materials. - M.: Science, 1986. - 512 p. Laboratory work № 2
“Analysis of the buckling bar resistance”
Introduction
At equibalance or bodies movement, temporary additional small agitation arises. Depending on the state the body acquires after the agitation, it is said that a body is in a stable or unstable state. The mathematical theory of stability was developed by A.M.Lyapunov, the buckling bar resistance was researched by L. Euler. Stable, indifferent equilibrium and unstable equilibrium can be shown by the example of three states of the ball equilibria. A ball is put on the bottom of the pit, and then it is replaced a bit and released. After some balancing the ball returns to the initial position. In the second test a ball is put on the horizontal surface and then it is replaced a bit. After the ball is released, it remains in the initial position. Finally, the ball is put on the top of the bumpy surface and then it is replaced a bit. The ball goes down and does not return to the initial position. These tests show: the first state of equilibrium is stable, the second state of equilibrium is indifferent, and the third state of equilibrium is unstable. Therefore aside strength and hardness provision, it is necessary to calculate the structural stability. Theory
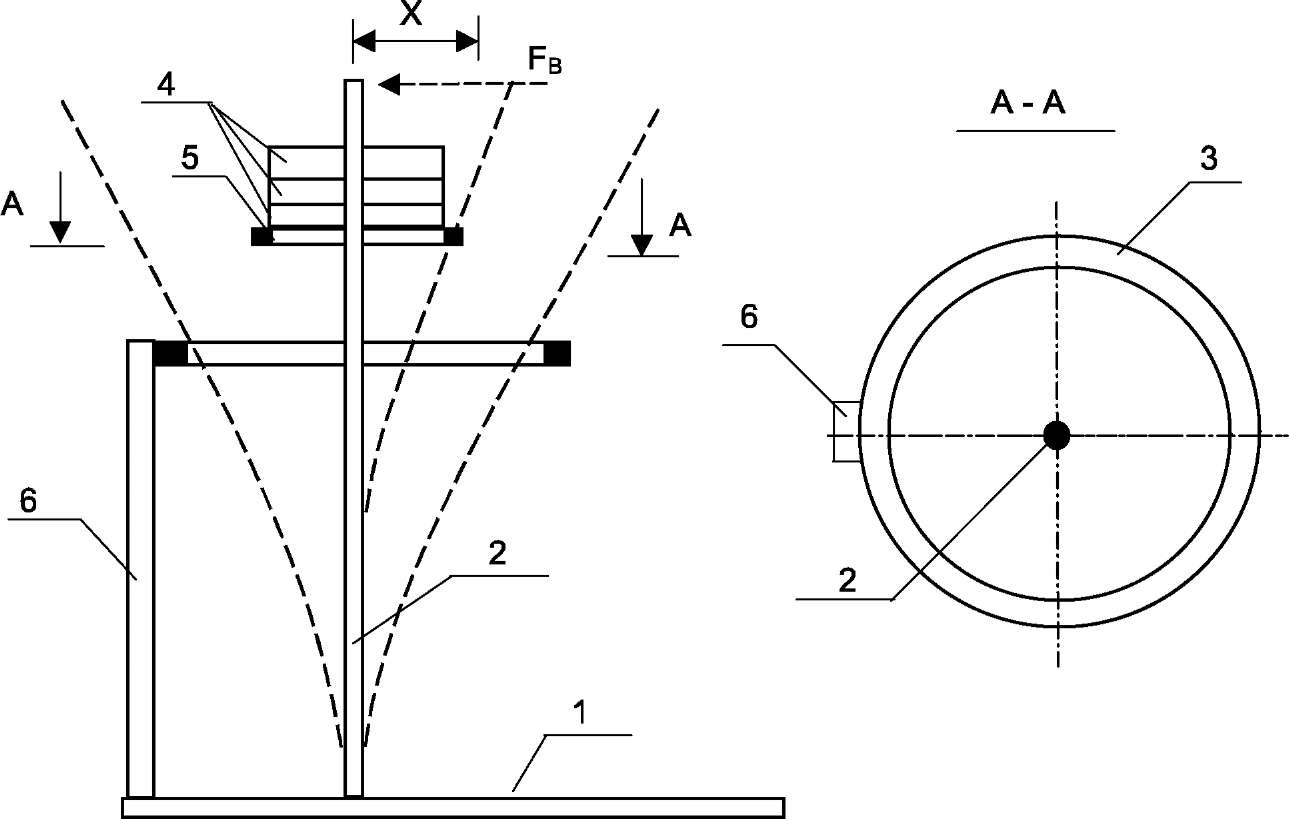
The stability is understood as the system property to keep its state under external actions. The stability of the initial equilibrium shape is a special case of the general stability. If this property does not remain, the system will be unstable. Let us imagine the following perfect system. The homogeneous bar, having the constant cross section, is subjected to axial compression (Fig.1). We gradually increase the axial force adding loads 4 and apply the temporary Fв force normal to the bar axis.
Fig. 1. Modelling stable and unstable states of the compression bar 1 - base, 2 - test bar 3 - restrictive ring, 4 - loads, 5 - load place, 6 - upright
Under the initial values of a compressive force the bar goes to the rectilinear eguilibrium shape bringing to effect some oscillations (dotted axes), lateral force removed. In this case the elastic strain energy of the bending is greater than the work of the compressive force causing the curvature of the bar. The subsequent increase of the compressive load (adding loads 4) may cause such a state of the bar under which the bar does not bring to effect the initial rectilinear shape and remains curved after the lateral temporary force has been acted. This new equilibrium state (under the absence of the material yield) is more complicated unlike the first one, because there also arise the bending stresses. There is the some critical intermediate position between these two positions and the load corresponding to it is critical. There is a theoretical possibility of the rectilinear equilibrium shape but it is unstable and transfers into a new equilibrium state, a curved one, under the smallest action. L. Euler defined the critical force as capable to keep a bar in a slightly curved state whose axis is given by the differential equation
where E is the modulus of elasticity, Imin is the minimum second moment of the cross-sectional area, F is the axial compressive force, y is the bar deflection. We get the critical force by solving the equation (1):
where
Fig. 2. Schemes of the bar ends clampty
On the basis of the above given notions, the experimentally determined Fcr value differs from the one calculated by the formula (2). The reason is the initial imperfection of the testing specimen. The initial bar deflection is referred here, the eccentrical force action on account of the variable cross - section along the length of the bar and the support construction, the material heterogeneity. That is why to experimentally determine the critical force Fcr, it is reasonable to apply Southwell’s method, which makes it possible to decrease the influence caused by the initial imperfections essentially. It should be kept in mind, that in real cases even with the loads lesser than the critical ones, we are to have the bended equelibrium shape of a bar. Let us consider Southwell’s method on the example of a pin-ended bar with a primary deflection (Fig.2a). The experience shows that the initial axis shape of the curved bar before its loading can be with sufficient accuracy given by the equation
where f0 is the initial bar bending deflection, Z is the distance between the section and the coordinate origin,
Let us assume that the additional bar deflections У 1, caused by the action of the compressive force F, also change all along its length by the sine law
where f1 is the additional bar deflection. Then
У=У0 + У1 (5)
Let us substitute into the equation (1) the expression (5) and then having solved it as related to f1, we get
Considering the formula (2), it follows
Let us divide the left and right parts of the expression (7) by
When conducting the experience we measure the deflection, depending on the force change F i.e. we receive
Comparing the expressions (8) and (9) we can conclude that the expression (8) is the equation of the straight line with the angular coefficient
cutting on the piece on the ordinate axis
This straight line is shown in Fig.3.
From formula (10) and Fig.3 it follows that the value of the critical force
We can also obtain an analogical result with the eccentricity load.
|

 (1)
(1) (2)
(2) - is the bar length,
- is the bar length, - is the coefficient dependent upon the way of clamping the bar ends. Some types of the bar ends clampty and the
- is the coefficient dependent upon the way of clamping the bar ends. Some types of the bar ends clampty and the 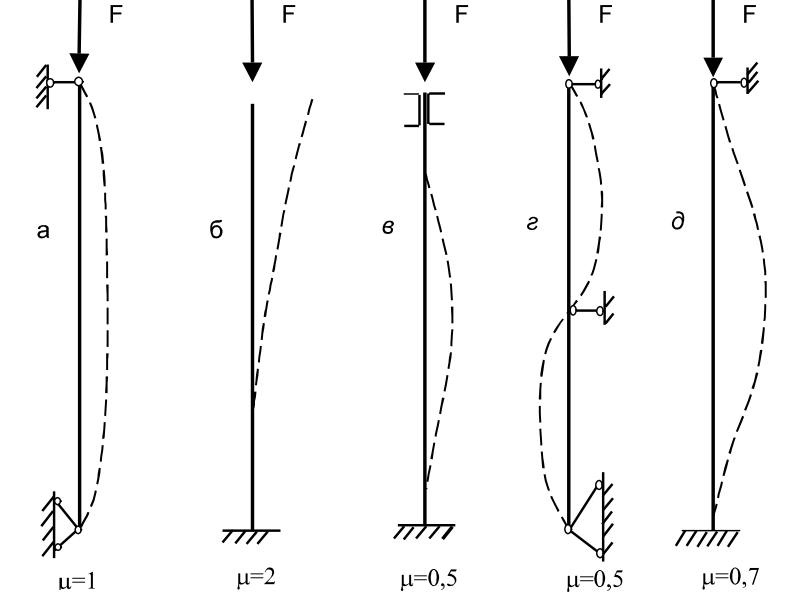
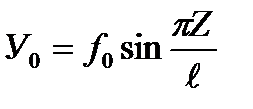 (3)
(3) is the bar length.
is the bar length.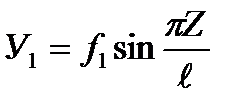 (4)
(4) (6)
(6) (7)
(7) and transform it to the form
and transform it to the form (8)
(8) (9)
(9) (10)
(10) (11)
(11) Fig.3. The relation graphic given by the formula (9)
Fig.3. The relation graphic given by the formula (9)
 (12)
(12)


