Уравнение мощностей
Для вывода уравнения мощностей используем теорему живых сил: мощность потока кинетической энергии системы равна сумме мощностей потоков всех внешних и внутренних сил, действующих в системе. Или математически
Рассмотрим левую часть уравнения (44). Здесь
где То- суммарная кинетическая энергия; Т -кинетическая энергия деталей, движущихся в поступательном движении; Т' - кинетическая энергия деталей, движущихся в относительном движении; δ - коэффициент вращающихся масс или отношение полной кинетической энергии системы к кинетической энергии ее поступательного движения. Для поступательного движения можно записать:
Но так как согласно выражению (45)
Продеффиринцировав выражение (47), получим
Таким образом, полученное нами выражение (48) является левой частью выражения (44). Получим теперь расчетные зависимости для правой части выражения (44). Рассмотрим мощности внешних сил Nвш. Внешними силами, работу которых следует учитывать, являются силы сопротивления движению: воздуха, на крюке, а также сила тяги. Здесь уместно напомнить, что действие силы инерции (Pj) и инерционного момента (Mj), приложенных к автомобилю в соответствии с принципом Даламбера, учтено кинетической энергией автомобиля. Силы, направленные перпендикулярно к плоскости дороги, при принятых ранее условиях работу не совершают. Работа моментов Mf от нормальных реакций дороги не должна учитываться, поскольку в силу сопротивления качению включены касательные реакции дороги. Тогда мощность сил сопротивления NR выразится произведением суммы этих сил на скорость поступательного движения
NR = - (Pψ + Pw + Pкр) σ Uо, (49)
где σ - коэффициент проскальзывания. Знак минус берется потому, что направления сил и скорости противоположны. Сила тяги совершает работу лишь при наличии проскальзывания (буксования) ведущих колес. Мощность силы тяги (P) определится ее произведением на абсолютную скорость точек опорной площадки
Np = - P (Uo – U). Заменив переносную скорость (U) через относительную (Uo), получим
Np = - PUo (1 – σ). (50)
Из уравнения равновесия получим
Подставив выражение (28) в выражение (27), получим
Складывая выражения (51) и (50), получим (∑ Nвш = NR + NP)
Из этого выражения следует, что мощность сил сопротивления (NR) не зависит от проскальзывания колес. Первый член в правой части уравнения обращается в нуль при отсутствии проскальзывания (σ = 1). Таким образом, при отсутствии проскальзывания колес получим
Рассмотрим теперь мощности внутренних сил. Мощность потока внутренних сил в наиболее общем виде определяется суммой мощности силовой установки
где Njд - инерционная мощность деталей силовой установки. Здесь
где θ д – момент инерции деталей силовой установки, приведенный к коленчатому валу двигателя (сюда же включается момент инерции деталей сцепления); iт – общее передаточное число силовой передачи автомобиля.
Теперь выражение (55) можно записать в следующем виде
Таким образом, найдены значения всех величин в правой части выражения (44). Подставив их, сгруппировав члены, содержащие ускорение (в левой части), и поделив уравнение почленно на относительную скорость ведущего колеса Uо, получим
Обозначим выражение в квадратных скобках через δ и назовем его коэффициентом вращающихся масс.
Обозначим также
Величина Рд, выражающая отношение мощности двигателя (за вычетом потерь) к относительной скорости, называется силой тяги (или окружным усилием) по двигателю. В действительности она не является ни внешней силой, ни силой вообще, хотя и имеет размерность силы.
С учетом принятых обозначений уравнение (58) будет иметь вид
Это и есть уравнение мощностей для автопоезда. При Ркр = 0 получим уравнение мощностей для одиночного автомобиля. В литературе это уравнение называется также уравнением тягового баланса. Таким образом, в главе мы рассмотрели расчетную схему прямолинейного движения автомобиля в общем случае (на подъеме) и установили при этом, какие силы и моменты действуют на автомобиль. Мы рассмотрели природу этих сил, а также установили математические зависимости для их определения. Знание и определение (количественное) этих сил необходимо для оценки процессов движения автомобиля. Мы также рассмотрели методику определения нормальных реакций на колесах двухосного и трехосного автомобиля. Наличие уравнений динамики позволяет, имея характеристику двигателя и заданные внешние условия, определить силу тяги и ускорение автомобиля.
|

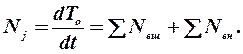 (44)
(44) , (45)
, (45) (46)
(46) , то, используя выражение (46), можно записать
, то, используя выражение (46), можно записать (47)
(47) (48)
(48)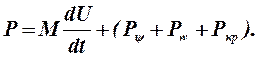 (51)
(51) (52)
(52) (53)
(53) (54)
(54) и мощности потерь Nt
и мощности потерь Nt (55)
(55)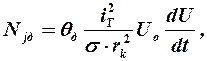 (56)
(56) (57)
(57) (58)
(58) (59)
(59) (60)
(60)


