Електричне поле
Електричні заряди наділяють простір, що оточує їх, особливими фізичними властивостями - створюють електричне поле. Основною властивістю поля є те, що на заряджене тіло, що знаходиться в цьому полі, діє сила, тобто взаємодія заряджених тіл здійснюється за допомогою електричних полів. Характеристикою електричного поля є векторна величина Е напруженість поля. Напруженість чисельно дорівнює силі, яка діє на одиничний пробний заряд.
. (3.4)
Рисунок 3.4. На рисунку 3.4 показані напрями векторів напруженості електричного поля позитивного і негативного точкового заряду. З малюнка видно, що вектор напруженості спрямований від заряду, якщо заряд позитивний і до заряду, якщо заряд негативний. Принцип суперпозиції електричного поля. Якщо електричне поле створюється декількома зарядами, то напруженість результуючого поля в цій точці визначається векторною сумою напруженостей кожного заряду.
Рисунок 3.5.
. (3.5)
де dE - елементарна напруженість електричного поля елементарного заряду dq. Приклад розв’язку задачі: Розрахувати напруженість електричного поля в точці, віддаленій на 1 см від центру рівномірно зарядженого тонкого стержня завдовжки 1 м Заряд стержня дорівнює Розв’язок.
dq dl
Так, як довжина стержня l набагато більша відстані r0 α 1 прагне до нуля, α 2 прагне до 180°.
Тоді. У розрахунках було прийнято, що заряджене тіло знаходилося у вакуумі (чи повітрі) ε =1 § 40. Потік вектора напруженості електричного поля. Теорема Гауса для електричного поля у вакуумі Експериментально встановлені закон Кулона і принцип суперпозиції дозволяють повністю описати електростатичне поле заданої системи зарядів. Проте, властивості електростатичного поля можна виразити в іншій, загальнішій формі, не удаючись до уявлення про кулонівське поле точкового заряду. Лінії напруженості електричного поля Для зручності і наочності електричне поле часто зображують графічно за допомогою силових ліній напруженості. Це лінії, дотичні до яких в кожній точці співпадають з напрямом вектора напруженості. Лініям напруженості приписують напрям, співпадаючий з напрямом вектора напруженості, вони завжди починаються на позитивному заряді і закінчуються на негативному. Оскільки в кожній цій точці простору вектор напруженості має лише один напрям, то лінії напруженості ніколи не перетинаються. На рисунку 3.6. показані лінії напруженості електричного поля.
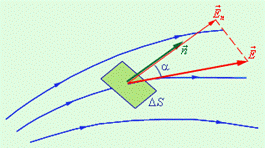
Рисунок 3.6. Силові лінії проводяться в такій кількості, щоб для будь-якої області поля виконувалася наступна чисельна рівність: число силових ліній, що пронизують одиницю площі поверхні, перпендикулярну лініям напруженості, має дорівнювати модулю вектора Е. Введемо нову фізичну величину, що характеризує електричне поле - потік Φ вектора напруженості електричного поля. Нехай в просторі, де створено електричне поле, розташований деякий досить малий майданчик Δ S. Добуток модуля вектора Е на площу Δ S і на косинус кута α між вектором Е і нормаллю n до майданчика називається елементарним потоком вектора напруженості через майданчик Δ S (рис. 3.7): Δ Φ = EΔ S cos α = EnΔ S, або dΦ =EndS. (3.6)
Рисунок 3.7. Розглянемо тепер деяку довільну замкнуту поверхню S (рис 3.8). Якщо розбити цю поверхню на малі майданчики Δ Si, і визначити елементарні потоки Δ Φ i поля E через ці малі майданчики, а потім їх підсумувати, то в результаті ми отримаємо потік Φ вектора E через замкнуту поверхню S:
У разі замкнутої поверхні завжди вибирається зовнішня нормаль.
Рисунок 3.8. Теорема Гауса стверджує: Потік вектора напруженості електростатичного поля у вакуумі через довільну замкнуту поверхню дорівнює сумі зарядів, розташованих усередині цієї поверхні поділену на електричну сталу ε 0.
Використовуючи теорему Гауса, можна у ряді випадків легко розрахувати напруженість електричного поля навколо зарядженого тіла, якщо заданий розподіл зарядів має яку-небудь симетрію. Знайдемо напруженість поля тонкостінного полого однорідно-зарядженого довгого циліндра радіусу R. З міркувань симетрії, електричне поле має бути спрямоване по радіусу. Тому для застосування теореми Гауса доцільно вибрати замкнуту поверхню S у вигляді співвісного циліндра деякого радіусу r і довжини L, закритого з обох торців (рис 3.9).
Рисунок 3.9. При r ≥ R увесь потік вектора напруженості проходитиме через бічну поверхню циліндра, площа якої дорівнює 2π rL, оскільки потік через обидві основи дорівнює нулю. Застосування теореми Гауса дає:
де τ = q/L - лінійна густина заряду. Цей результат не залежить від радіусу R зарядженого циліндра, тому він може застосовуватися і до поля довгої однорідної зарядженої нитки. Для визначення напруженості поля усередині зарядженого циліндра треба побудувати замкнуту поверхню для випадку r < R. В даному випадку потік вектора напруженості через бічну поверхню циліндра гауса має бути і в цьому випадку рівний Φ = E2π rL. Згідно з теоремою Гауса, цей потік пропорційний заряду, що виявився усередині замкнутої поверхні. Цей заряд дорівнює нулю. Звідси витікає, що електричне поле усередині однорідно-зарядженого довгого порожнистого циліндра дорівнює нулю. Аналогічним чином можна застосувати теорему Гауса для визначення електричного поля у ряді інших випадків, коли розподіл зарядів має яку-небудь симетрію. У кожному з таких випадків треба вибирати замкнуту поверхню доцільної форми. Наприклад, у разі центральної симетрії поверхню зручно вибирати у вигляді сфери з центром в точці симетрії. При осьовій симетрії замкнуту поверхню треба вибирати у вигляді співвісного циліндра, замкнутого з обох торців (як в розглянутому вище прикладі). Якщо розподіл зарядів не має якої-небудь симетрії і загальну структуру електричного поля вгадати неможливо, застосування теореми Гауса не може спростити завдання визначення напруженості поля. Розглянемо ще один приклад симетричного розподілу зарядів - визначення поля рівномірно зарядженої площини (рис. 3.10).
В цьому випадку поверхню Гауса S доцільно вибрати у вигляді циліндра деякої довжини, закритого з обох торців. Вісь циліндра спрямована перпендикулярно зарядженій площині, а його торці розташовані на однаковій відстані від неї. Через симетрію поле рівномірно зарядженої площини має бути скрізь спрямоване по нормалі. Застосування теореми Гауса дає:
де σ =q/S - поверхнева густина заряду, тобто заряд, що приходиться на одиницю площі. Отриманий вираз для електричного поля однорідної зарядженої площини можна застосувати і у разі плоских заряджених площин кінцевого розміру. В цьому випадку відстань від точки, в якій визначається напруженість поля, до зарядженої площини має бути значно менша розмірів площини. §41. Робота електричного поля по переміщенню заряду. Потенціал При переміщенні пробного заряду q в електростатичному полі електричні сили здійснюють роботу (рис. 3.11). Ця робота при малому переміщенні Δ l становить:
Рисунок 3.11. Розглянемо роботу сил електростатичного поля по переміщенню точкового заряду.
. (3.12)
Рисунок 3.12.
. (3.13)
Отриманий результат не залежить від форми траєкторії. На траєкторіях I і II, зображених на рисунку 3.12, роботи кулонівських сил однакові. Якщо на одній з траєкторій змінити напрям переміщення заряду q на протилежне, то робота змінить знак. Звідси витікає, що на замкнутій траєкторії робота кулонівських сил дорівнює нулю. Отже електростатичне поле має важливу властивість: Робота сил електростатичного поля при переміщенні заряду з однієї точки поля в іншу не залежить від форми траєкторії, а визначається тільки положенням початкової і кінцевої точок і величиною заряду. Наслідком незалежності роботи від форми траєкторії є наступне твердження: Робота сил електростатичного поля при переміщенні заряду по будь-якій замкнутій траєкторії дорівнює нулю. Силові поля, що мають цю властивість, називають потенціальними або консервативними. В тому випадку, коли електростатичне поле створюється сукупністю точкових зарядів Qi, то при переміщенні пробного заряду q робота результуючого поля A відповідно до принципу суперпозиції складатиметься з робіт Ai кулонівських полів точкових зарядів:
Оскільки кожен член суми Ai не залежить від форми траєкторії, то і повна робота A результуючого поля не залежить від шляху і визначається тільки положенням початкової і кінцевої точок. Властивість потенціальності електростатичного поля дозволяє ввести поняття потенціальної енергії заряду в електричному полі. Для цього в просторі вибирається деяка точка (0), і потенціальна енергія заряду q, поміщеного в цю точку, приймається рівною нулю. Потенціальна енергія заряду q, поміщеного в будь-яку точку (1) простору, відносно фіксованої точки (0) дорівнює роботі A10, яку виконає електричне поле при переміщенні заряду q з точки (1) в точку (0): Wp1 = A10. (В електростатиці енергію прийнято означати буквою W, оскільки буквою E позначають напруженість поля.) Так само, як і в механіці, потенціальна енергія визначена з точністю до сталої величини, залежної від вибору опорної точки (0). Така неоднозначність у визначенні потенціальної енергії не призводить до яких-небудь непорозумінь, оскільки фізичний зміст має не сама енергія, а різниця її значень в двох точках простору. Робота, що здійснюється електричним полем при переміщенні точкового заряду q з точки (1) в точку (2), дорівнює різниці значень потенціальної енергії в цих точках і не залежить від шляху переміщення заряду і від вибору точки (0). A12 = A10 + A02 = A10 - A20 = Wp1 - Wp2. (3.14)
. (3.15) Потенціал φ є енергетичною характеристикою електростатичного поля. Робота A12 по переміщенню електричного заряду q з початкової точки (1) в кінцеву точку (2) дорівнює добутку заряду на різницю потенціалів (φ 1 - φ 2) початкової і кінцевої точок A12 = Wp1 - Wp2 = qφ 1 - qφ 2 = q(φ 1 - φ 2). (3.16) У Міжнародній системі одиниць (СІ) одиницею потенціалу являється вольт (В). 1 В = 1 Дж / 1 Кл. У багатьох завданнях електростатики при обчисленні потенціалів за опорну точку (0) зручно прийняти нескінченно віддалену. В цьому випадку поняття потенціалу може бути визначене таким чином:
Для наочного представлення електричного поля разом з силовими лініями використовують еквіпотенціальні поверхні. Поверхня, в усіх точках якої потенціал електричного поля має однакові значення, називається еквіпотенціальною поверхнею або поверхнею рівного потенціалу. Силові лінії електричного поля завжди перпендикулярні еквіпотенціальним поверхням. На рисунку 3.13 представлені картини силових ліній і еквіпотенціальних поверхонь деяких простих електростатичних полів.
Рисунок 3.13. Еквіпотенціальні поверхні (сині лінії) і силові лінії (червоні лінії) простих електричних полів: a - точковий заряд; b - електричний диполь; c - два рівні позитивні заряди. У разі однорідного поля еквіпотенціальні поверхні є системою паралельних площин. Якщо пробний заряд q переміщується на відстань Δ r уздовж силової лінії з точки (1) в точку (2), то елементарна робота сил поля дорівнює: Δ A12 = qEΔ r= q(φ 1 – φ 2) = – qΔ φ,
З відси слідує, що (3.17) Вираз (3.17) в скалярній і векторній формі виражає зв'язок між напруженістю поля і потенціалом. Потенціал φ поля точкового заряду Q на відстані r від нього відносно нескінченно віддаленої точки обчислюється таким чином:
. (3.18)
Як випливає з теореми Гауса, ця ж формула виражає потенціал поля рівномірно зарядженої кулі (чи сфери) при r ≥ R, де R - радіус кулі. З принципу суперпозиції напруженості електричного поля, слідує принцип суперпозиції для потенціалів: φ = φ 1 + φ 2 + φ 3 +.. § 42. Діелектрики і провідники в електричному полі. Поляризація діелектриків. Електроємність. Конденсатори Діелектрики (ізолятори) складаються з нейтральних атомів і молекул. На відміну від металів, електрони в атомах діелектрика сильно пов'язані зі своїми ядрами. Тому вони не можуть переміщатися під дією електричного поля по усьому об'єму діелектрика. Це означає, що діелектрики не здатні проводити електричний струм. Існує 2 типи діелектриків: полярні і неполярні. У молекулі полярного діелектрика центри " тяжіння" негативно заряджених електронів і позитивно заряджених ядер атомів, що входять до складу молекули, не співпадають. Таку молекулу можна розглядати як електричний диполь (сукупність двох рівних по модулю різнойменних точкових зарядів, розташованих на деякій відстані один від одного). Диполь характеризується векторною величиною
У молекулі неполярного діелектрика центри " тяжіння" негативних і позитивних зарядів співпадають. Тому дипольний момент такої молекули дорівнює нулю, а значить і результуючий момент неполярного діелектрика також дорівнює нулю. Розглянемо тепер, що станеться з полярним діелектриком, якщо помістити його в зовнішнє електричне поле у вакуумі, напруженість якого становить Е0. Сили зовнішнього поля прагнутимуть повернути диполі молекул діелектрика уздовж поля і результуючий дипольний момент усього діелектрика вже буде відмінний від нуля ( Якщо в зовнішнє електричне поле помістити неполярний діелектрик, то пов'язані заряди кожної молекули діелектрика змістяться в протилежні сторони, утворюючи електричні диполі. Результуючий дипольний момент усього діелектрика буде відмінний від нуля ( До провідників відносяться тіла, в яких є вільні (не пов'язані) електричні заряди. Зокрема, в металах вільними електричними зарядами є валентні електрони атомів, з яких складається метал. У звичайному стані вільні заряди провідників хаотично переміщаються по усьому об’єму тіла. Внесення провідника в зовнішнє електричне поле викличе впорядкований рух вільних зарядів під дією сил цього поля: позитивні заряди рухатимуться у напрямі поля (тобто у напрямі вектора Якщо нейтральному провідник має надмірні вільні заряди, вони повинні розподілитися по провідникові так, щоб електричне поле усередині провідника було відсутнє. Відповідно потенціал в будь-якій точці провідника, включаючи поверхню провідника, буде однаковим. Застосовуючи теорему Гауса (3.8) для простору усередині провідника, де поле відсутнє (Е=0), отримаємо: Електрична ємність Якщо двом ізольованим один від одного провідникам передати заряди q1 і q2, то між ними виникає деяка різниця потенціалів Δ φ;, залежна від величин зарядів і геометрії провідників. Різницю потенціалів Δ φ між двома точками в електричному полі часто називають напругою і позначають буквою U. Найбільший практичний інтерес представляє випадок, коли заряди провідників однакові по модулю і протилежні за знаком. В цьому випадку можна ввести поняття електричної ємності.
У СІ одиниця електроємності називається фарад (Ф):. Електроємність залежить від форми і розмірів провідників і від властивостей діелектрика, що розділяє провідники. Існують такі конфігурації провідників, при яких електричне поле виявляється зосередженим (локалізованим) лише в деякій області простору. Такі системи називаються конденсаторами, а провідники, що становлять конденсатор, називаються обкладками.
Рисунок 3.14. Рисунок 3.15. Кожна із заряджених пластин плоского конденсатора створює поблизу поверхні електричне поле, модуль напруженості якого виражається співвідношенням (3.10)
Згідно з принципом суперпозиції, напруженість поля Е, що створюється обома пластинами, дорівнює сумі напруженостей Е+ і Е- полів кожної з пластин: Е=Е++Е-.
. (3.20)
(3.21)
(3.22) Прикладами конденсаторів з іншою конфігурацією обкладок можуть служити сферичний і циліндричний конденсатори. Сферичний конденсатор - це система з двох концентричних сфер радіусів R1 і R2. Циліндричний конденсатор - система з двох співісних циліндрів радіусів R1 і R2 і довжини L. Ємності цих конденсаторів, заповнених діелектриком з діелектричною проникністю ε;, виражаються формулами:
З'єднання конденсаторів
, (3.23) Таким чином, при паралельному з'єднанні електроємності складаються.
Рисунок 3.16. Рисунок 3.17.
(3.24) При послідовному з'єднанні конденсаторів складаються зворотні величини ємностей. Формули для паралельного і послідовного з'єднання залишаються справедливими при будь-якому числі конденсаторів, сполучених в батарею. §43. Енергія електричного поля Дослід показує, що заряджений конденсатор містить запас енергії. Енергія зарядженого конденсатора дорівнює роботі зовнішніх сил, яку необхідно витратити, щоб зарядити конденсатор.
. (3.25)
Рисунок 3.18.
(3.26) Електричну енергію We слід розглядати як потенціальну енергію, запасену в зарядженому конденсаторі.
E = U/d, а його ємність, тоді
(3.28) є електричною (потенціальною) енергією одиниці об'єму простору, в якому створено електричне поле. Її називають об'ємною густиною електричної енергії. Приклад розв’язку задачі: Електричне поле створене рівномірно розподіленим по кільцю зарядом
Питання і завдання 1. Що таке електричне поле? Яка фізична величина є характеристикою електричного поля? Що таке лінійна, поверхнева і об'ємна густини зарядів? 2. Що називається силовими лініями електричного поля, як вони проводяться? 3. Що таке потік вектора напруженості електричного поля. Сформулюйте теорему Гауса. 4. Як довести, що електричне поле є потенціальним? Дайте визначення потенціалу даної точки електричного поля і різниці потенціалів. 5. Що таке еквіпотенціальна поверхня. Чому дорівнює робота сил електричного поля по переміщенню заряду уздовж еквіпотенціальної поверхні? 6. Що таке поляризація діелектриків. У чому відмінність поляризації діелектриків з полярними і не полярними молекулами? 7. Що відбувається з провідниками при внесенні їх в електричне поле? 8. На двох тонких нитках завдовжки 1м, підвішених до одного гачка, висять дві маленькі кульки однакової маси. Після передачі кулькам однакових зарядів 2, 5· 10-6 Кл вони розійшлися, причому нитки утворили кут 60°. Знайти масу кульок. (10 г). 9. Який заряд має порошинка вагою 6·10-11Н, якщо вона урівноважена в електричному полі, напруженість якого дорівнює 3·105 В/м? (2·10-16 Кл). 10. У двох вершинах рівностороннього трикутника із стороною 10 см знаходяться однакові точкові заряди 1 нКл. Знайти напруженість електричного поля в третій вершині.(1566 В/м). 11. Розрахувати напруженість електричного поля в точці, віддаленій на 1 см від кінця рівномірно зарядженого тонкого стержня завдовжки 1 м Заряд стержня дорівнює 1 нКл.(891 В/м). 12. Використовуючи теорему Гауса розрахуйте напруженість електричного поля на відстані 1 см від нескінченної зарядженої нитки з лінійною густиною заряду 13. З якою силою взаємодіє точковий заряд 1 нКл з нескінченною зарядженою ниткою? Лінійна густина заряду нитки 8 мкКл/м, відстань між ниткою і зарядом 14. Використовуючи теорему Гауса розрахуйте напруженість електричного поля рівномірно зарядженої кулі з об'ємною густиною заряду 5 нКл/м3 і радіусом 10 см на відстані 2см і 12 см від центра кулі. Побудувати графік залежності Е(r)? (3, 8В/м, 13 В/м). 15. Використовуючи теорему Гауса розрахуйте напруженість електричного поля рівно
|

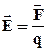 . (3.3)
. (3.3) Якщо електричне поле створене точковим зарядом, то величину напруженості поля можна розрахувати по формулі
Якщо електричне поле створене точковим зарядом, то величину напруженості поля можна розрахувати по формулі





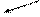


 .
.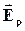 На рисунку 3.5 показана напруженість результуючого поля двох точкових зарядів q1 і q2 в точці О.
На рисунку 3.5 показана напруженість результуючого поля двох точкових зарядів q1 і q2 в точці О.



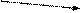
 О
О 
 q1
q1 

 q2
q2 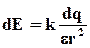 У тому випадку, коли заряджене тіло не можна вважати точковим, формулу напруженості електричного поля треба записувати в диференціальному виді.
У тому випадку, коли заряджене тіло не можна вважати точковим, формулу напруженості електричного поля треба записувати в диференціальному виді.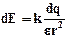 В даному випадку заряджене тіло не можна вважати точковим зарядом, тому для вирозв’язку задачі поступимо таким чином. Заряджений стержень подумки розіб'ємо на нескінченно малі ділянки завдовжки dl, кожна ділянка стержня містить заряд dq і в точці О електричного поля створює напруженість
В даному випадку заряджене тіло не можна вважати точковим зарядом, тому для вирозв’язку задачі поступимо таким чином. Заряджений стержень подумки розіб'ємо на нескінченно малі ділянки завдовжки dl, кожна ділянка стержня містить заряд dq і в точці О електричного поля створює напруженість

 r r0
r r0

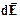
 О
О

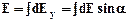

 Далі необхідно перетворити вираз щоб прийти до однієї змінної інтегрування. Введемо поняття лінійної густини заряду тоді dq=τ dl,
Далі необхідно перетворити вираз щоб прийти до однієї змінної інтегрування. Введемо поняття лінійної густини заряду тоді dq=τ dl,
 ,
,

 .
.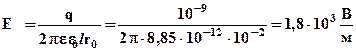

 . (3.7)
. (3.7)
 (3.8)
(3.8)

 (3.9)
(3.9)
 (3.10)
(3.10) . (3.11)
. (3.11)
 На рисунку 3.12 зображені силові лінії кулонівського поля точкового заряду Q і дві різні траєкторії переміщення пробного заряду q з початкової точки (1) в кінцеву точку (2). На одній з траєкторій виділено мале переміщення Δ l. Елементарна робота Δ A кулонівських сил на цьому переміщенні дорівнює:
На рисунку 3.12 зображені силові лінії кулонівського поля точкового заряду Q і дві різні траєкторії переміщення пробного заряду q з початкової точки (1) в кінцеву точку (2). На одній з траєкторій виділено мале переміщення Δ l. Елементарна робота Δ A кулонівських сил на цьому переміщенні дорівнює: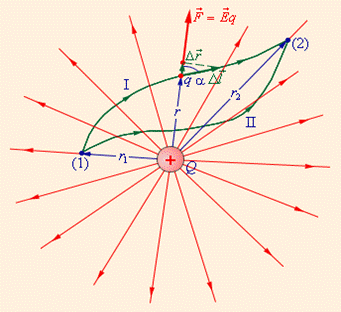
 Якщо вираз (3.12) проінтегрувати на інтервалі від r = r1 до r = r2, отримаємо повну роботу:
Якщо вираз (3.12) проінтегрувати на інтервалі від r = r1 до r = r2, отримаємо повну роботу: .
. Фізичну величину, рівну відношенню потенціальної енергії електричного заряду в електростатичному полі до величини цього заряду, називають потенціалом φ електричного поля:
Фізичну величину, рівну відношенню потенціальної енергії електричного заряду в електростатичному полі до величини цього заряду, називають потенціалом φ електричного поля: Потенціал поля в заданій точці простору дорівнює роботі, яку здійснюють електричні сили пр переміщенні одиничного позитивного заряду з цієї точки в безкінченність.
Потенціал поля в заданій точці простору дорівнює роботі, яку здійснюють електричні сили пр переміщенні одиничного позитивного заряду з цієї точки в безкінченність.


 , яка називається дипольним електричним моментом. По модулю дипольний момент дорівнює абсолютному значенню заряду, помноженому на відстань між зарядами. За напрям вектора
, яка називається дипольним електричним моментом. По модулю дипольний момент дорівнює абсолютному значенню заряду, помноженому на відстань між зарядами. За напрям вектора 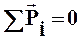 .
. ). Внаслідок цього на протилежних гранях діелектрика з'являться пов'язані заряди протилежного знаку, що приведе до виникнення власного електричного поля напруженістю Е, спрямованого проти зовнішнього поля. Напруженість результуючого поля Ер усередині діелектрика буде рівна Е0 - Е. Таким чином, результуюче поле усередині діелектрика буде ослабленим в порівнянні з полем у вакуумі. Величина діелектричної проникності діелектрика (якраз і показує в скільки разів ослабляється поле усередині діелектрика в порівнянні з полем у вакуумі (e=Е0/Е). Розглянуте явище появи різнойменних пов'язаних зарядів на протилежних гранях полярного діелектрика при внесенні його в зовнішнє електричне поле називається поляризацією діелектрика.
). Внаслідок цього на протилежних гранях діелектрика з'являться пов'язані заряди протилежного знаку, що приведе до виникнення власного електричного поля напруженістю Е, спрямованого проти зовнішнього поля. Напруженість результуючого поля Ер усередині діелектрика буде рівна Е0 - Е. Таким чином, результуюче поле усередині діелектрика буде ослабленим в порівнянні з полем у вакуумі. Величина діелектричної проникності діелектрика (якраз і показує в скільки разів ослабляється поле усередині діелектрика в порівнянні з полем у вакуумі (e=Е0/Е). Розглянуте явище появи різнойменних пов'язаних зарядів на протилежних гранях полярного діелектрика при внесенні його в зовнішнє електричне поле називається поляризацією діелектрика. ). Так само, як і у випадку з полярним діелектриком, станеться поляризація неполярного діелектрика, в результаті якої поле усередині діелектрика буде ослабленим в порівнянні з полем у вакуумі.
). Так само, як і у випадку з полярним діелектриком, станеться поляризація неполярного діелектрика, в результаті якої поле усередині діелектрика буде ослабленим в порівнянні з полем у вакуумі. ), негативні - в протилежну сторону (тобто проти напряму вектору
), негативні - в протилежну сторону (тобто проти напряму вектору 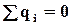 . Цей результат означає, що простір усередині провідника являється електрично нейтральним. Звідси витікає, що усі надмірні вільні заряди, які були передані провідникові, розташовуються на поверхні провідника.
. Цей результат означає, що простір усередині провідника являється електрично нейтральним. Звідси витікає, що усі надмірні вільні заряди, які були передані провідникові, розташовуються на поверхні провідника. Електроємністю системи з двох провідників називається фізична величина, яка визначається відношенням заряду q одного з провідників до різниці потенціалів Δ φ між ними:
Електроємністю системи з двох провідників називається фізична величина, яка визначається відношенням заряду q одного з провідників до різниці потенціалів Δ φ між ними: (3.19)
(3.19)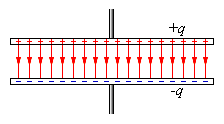 Простим конденсатором являється система з двох плоских пластин, розташованих паралельно одна одній на малій в порівнянні з розмірами пластин відстані і розділених шаром діелектрика. Такий конденсатор називається плоским. Електричне поле плоского конденсатора в основному локалізоване між пластинами (рис. 3.14); проте, поблизу країв пластинів і в навколишньому просторі також виникає порівняно слабке електричне поле, яке називають полем розсіяння. У цілому ряду завдань можна приблизно вважати, що електричне поле плоского конденсатора цілком зосереджене між його обкладками (рис. 3.15).
Простим конденсатором являється система з двох плоских пластин, розташованих паралельно одна одній на малій в порівнянні з розмірами пластин відстані і розділених шаром діелектрика. Такий конденсатор називається плоским. Електричне поле плоского конденсатора в основному локалізоване між пластинами (рис. 3.14); проте, поблизу країв пластинів і в навколишньому просторі також виникає порівняно слабке електричне поле, яке називають полем розсіяння. У цілому ряду завдань можна приблизно вважати, що електричне поле плоского конденсатора цілком зосереджене між його обкладками (рис. 3.15).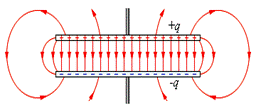
 .
. Усередині конденсатора вектори Е+ і Е - і паралельні; тому модуль напруженості сумарного поля рівний
Усередині конденсатора вектори Е+ і Е - і паралельні; тому модуль напруженості сумарного поля рівний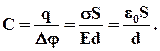 Поза пластинами вектори Е+ і Е- - спрямовані в різні боки, і тому E = 0. Поверхнева густина заряду пластин σ =q/S, де q - заряд, а S - площа кожної пластини. Різниця потенціалів між пластинами в однорідному електричному полі Δ φ =Ed, де d - відстань між пластинами. З цих співвідношень можна отримати формулу для електроємності плоского конденсатора:
Поза пластинами вектори Е+ і Е- - спрямовані в різні боки, і тому E = 0. Поверхнева густина заряду пластин σ =q/S, де q - заряд, а S - площа кожної пластини. Різниця потенціалів між пластинами в однорідному електричному полі Δ φ =Ed, де d - відстань між пластинами. З цих співвідношень можна отримати формулу для електроємності плоского конденсатора: Таким чином, електроємність плоского конденсатора прямо пропорційна площі пластин (обкладок) і обернено пропорційна до відстані між ними. Якщо простір між обкладками заповнений діелектриком, електроємність конденсатора збільшується в ε раз:
Таким чином, електроємність плоского конденсатора прямо пропорційна площі пластин (обкладок) і обернено пропорційна до відстані між ними. Якщо простір між обкладками заповнений діелектриком, електроємність конденсатора збільшується в ε раз:

 Конденсатори можуть з'єднуватися між собою, утворюючи батареї конденсаторів. При паралельному з'єднанні конденсаторів (рис. 3.16) напруги на конденсаторах однакові: U1 = U2 = U,, а заряди різні q1 = С1 U і q2 = С2 U. Таку систему можна розглядати як єдиний конденсатор електроємності C, заряджений зарядом q=q1+q2 при напрузі між обкладками рівному U. Звідси слідує:
Конденсатори можуть з'єднуватися між собою, утворюючи батареї конденсаторів. При паралельному з'єднанні конденсаторів (рис. 3.16) напруги на конденсаторах однакові: U1 = U2 = U,, а заряди різні q1 = С1 U і q2 = С2 U. Таку систему можна розглядати як єдиний конденсатор електроємності C, заряджений зарядом q=q1+q2 при напрузі між обкладками рівному U. Звідси слідує:

 При послідовному з'єднанні (рис. 3.17) однаковими виявляються заряди обох конденсаторів: q1=q2=q, а напруга на них різна U1 =q/C1 і U2 =q/C2 Таку систему можна розглядати як єдиний конденсатор, заряджений зарядом q при напрузі між обкладками
При послідовному з'єднанні (рис. 3.17) однаковими виявляються заряди обох конденсаторів: q1=q2=q, а напруга на них різна U1 =q/C1 і U2 =q/C2 Таку систему можна розглядати як єдиний конденсатор, заряджений зарядом q при напрузі між обкладками  Процес зарядки конденсатора можна представити як послідовне перенесення досить малих порцій заряду dq > 0 з однієї обкладки на іншу (рис. 3.18). При цьому одна обкладка поступово заряджається позитивним зарядом, а інша - негативним. Кожна порція dq переноситься в умовах, коли на обкладках вже є деякий заряд q, а між ними існує деяка різниця потенціалів. Тоді при перенесенні кожної порції dq зовнішні сили повинні виконати роботу
Процес зарядки конденсатора можна представити як послідовне перенесення досить малих порцій заряду dq > 0 з однієї обкладки на іншу (рис. 3.18). При цьому одна обкладка поступово заряджається позитивним зарядом, а інша - негативним. Кожна порція dq переноситься в умовах, коли на обкладках вже є деякий заряд q, а між ними існує деяка різниця потенціалів. Тоді при перенесенні кожної порції dq зовнішні сили повинні виконати роботу Енергія конденсатора ємності C, зарядженого зарядом Q, може бути знайдена шляхом інтегрування цього виразу в межах від 0 до Q:
Енергія конденсатора ємності C, зарядженого зарядом Q, може бути знайдена шляхом інтегрування цього виразу в межах від 0 до Q:
 Формулу, що виражає енергію зарядженого конденсатора, можна переписати в іншій формі, якщо скористатися співвідношенням Q = CU.
Формулу, що виражає енергію зарядженого конденсатора, можна переписати в іншій формі, якщо скористатися співвідношенням Q = CU. Розглянемо плоский конденсатор. Напруженість однорідного поля в плоскому конденсаторі рівна
Розглянемо плоский конденсатор. Напруженість однорідного поля в плоскому конденсаторі рівна (3.27)
(3.27) де V = Sd - об'єм простору між обкладками, зайнятий електричним полем. З цього співвідношення виходить, що фізична величина
де V = Sd - об'єм простору між обкладками, зайнятий електричним полем. З цього співвідношення виходить, що фізична величина =1 мкКл/м).Визначити роботу сил поля по переміщенню заряду Q=10 нКл з точки 1 (у центрі кільця) в точку 2, що знаходиться на перпендикулярі до площини кільця (Рисунок нижче).
=1 мкКл/м).Визначити роботу сил поля по переміщенню заряду Q=10 нКл з точки 1 (у центрі кільця) в точку 2, що знаходиться на перпендикулярі до площини кільця (Рисунок нижче).
 А1, 2 -?
А1, 2 -?







