3.1.Интегрирование рациональных функций
Рациональной функцией будем называть дробь вида 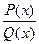 , где P(x) и Q(x) – многочлены. Если степень числителя меньше степени знаменателя, то дробь называется правильной; в противном случае – неправильной. Всякая правильная дробь может быть представлена в виде суммы простейших дробей; так называют дроби четырех типов:
, где P(x) и Q(x) – многочлены. Если степень числителя меньше степени знаменателя, то дробь называется правильной; в противном случае – неправильной. Всякая правильная дробь может быть представлена в виде суммы простейших дробей; так называют дроби четырех типов:  ;
;
 , где n – натуральное число, не равное единице;
, где n – натуральное число, не равное единице;  ;
;  , где n – натуральное число, не равное единице. Здесь А, В, а, p, q – числа; квадратные трехчлены x 2+ px + q не имеют действительных корней. Для того, чтобы представить правильную дробь
, где n – натуральное число, не равное единице. Здесь А, В, а, p, q – числа; квадратные трехчлены x 2+ px + q не имеют действительных корней. Для того, чтобы представить правильную дробь 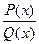 в виде суммы простейших дробей, надо, прежде всего, разложить знаменатель на линейные и квадратичные множители. Каждому простому линейному множителю соответствует в сумме простейших дробей дробь первого типа. Каждому линейному множителю кратности k соответствует дробь первого типа и (k –1) дробь второго типа: с показателями от 2 до k. Аналогично обстоит дело и с квадратичными множителями. Коэффициенты простейших дробей находятся методом неопределенных коэффициентов.
в виде суммы простейших дробей, надо, прежде всего, разложить знаменатель на линейные и квадратичные множители. Каждому простому линейному множителю соответствует в сумме простейших дробей дробь первого типа. Каждому линейному множителю кратности k соответствует дробь первого типа и (k –1) дробь второго типа: с показателями от 2 до k. Аналогично обстоит дело и с квадратичными множителями. Коэффициенты простейших дробей находятся методом неопределенных коэффициентов.
Разложение рациональной дроби в сумму простейших дробей используется для интегрирования. А именно, если дробь неправильная, то сначала ее представляют в виде суммы многочлена и правильной дроби, а затем правильную дробь представляют в виде суммы простейших дробей. Тогда для интегрирования рациональной дроби достаточно уметь интегрировать простейшие дроби. Дроби первого и второго типов интегрируются в общем виде:
ò  dx = А lnï x – а ï +С; ò
dx = А lnï x – а ï +С; ò  dx =
dx =  +С. Способы интегрирования дробей третьего и четвертого типа будут показаны на примерах.
+С. Способы интегрирования дробей третьего и четвертого типа будут показаны на примерах.
Примеры. 1) Проинтегрируем правильную дробь  . Разложим знаменатель на множители: х 4–4 х 3+4 х 2= х 2(х 2–4 х +4)= х 2(х –2)2. Значит, разложение дроби в сумму простейших содержит две дроби первого и две дроби второго типа:
. Разложим знаменатель на множители: х 4–4 х 3+4 х 2= х 2(х 2–4 х +4)= х 2(х –2)2. Значит, разложение дроби в сумму простейших содержит две дроби первого и две дроби второго типа:  =
=  +
+  +
+  +
+  . Приведем дроби в правой части к общему знаменателю и приравняем числители правой и левой части: х 3–2 х 2–3 х +4=А х (х –2)2+В(х –2)2+С х 2(х –2)+D х 2. Это равенство должно выполняться при всех значениях х. Подставив четыре различных значения х, получим уравнения, связывающие коэффициенты. При х =0: 4=4В; при х =2: –2=4D; при х =1: 0=А+В–С+D; при х = –1: 4= –9А+9В–3С+D. Отсюда В=1, D= –0, 5, А=0, 25, С=0, 75. Значит,
. Приведем дроби в правой части к общему знаменателю и приравняем числители правой и левой части: х 3–2 х 2–3 х +4=А х (х –2)2+В(х –2)2+С х 2(х –2)+D х 2. Это равенство должно выполняться при всех значениях х. Подставив четыре различных значения х, получим уравнения, связывающие коэффициенты. При х =0: 4=4В; при х =2: –2=4D; при х =1: 0=А+В–С+D; при х = –1: 4= –9А+9В–3С+D. Отсюда В=1, D= –0, 5, А=0, 25, С=0, 75. Значит,  =
=
 +
+  +
+  –
–  . А тогда ò
. А тогда ò  =0, 25lnï x ï –
=0, 25lnï x ï –  +0, 75lnï x –2ï +
+0, 75lnï x –2ï +  +C.
+C.
2) Проинтегрируем неправильную дробь  . Представим ее в виде (2 х –1)+
. Представим ее в виде (2 х –1)+  . Полученная правильная дробь – простейшая дробь третьего типа. Найдем производную ее знаменателя: (х 2–6 х +11)¢ =2 х –6. Теперь запишем числитель дроби в виде А(2 х –6)+В, получим: х –9=0, 5(2 х –6)–6, т.е. ò
. Полученная правильная дробь – простейшая дробь третьего типа. Найдем производную ее знаменателя: (х 2–6 х +11)¢ =2 х –6. Теперь запишем числитель дроби в виде А(2 х –6)+В, получим: х –9=0, 5(2 х –6)–6, т.е. ò  dx =
dx =
ò  dx =0, 5ò
dx =0, 5ò  –6ò
–6ò 
=0, 5ò  –6ò
–6ò  =
=
0, 5ln(x 2–6 x +11)–3  arctg
arctg  +C.
+C.
Окончательно ò  dx = ò (2 х –1) dx +
dx = ò (2 х –1) dx +
ò  dx = x 2– x +0, 5ln(x 2–6 x +11)–3
dx = x 2– x +0, 5ln(x 2–6 x +11)–3  arctg
arctg  +C.·
+C.· 
3.2.Интегрирование тригонометрических функций
Покажем на примерах некоторые способы интегрирования тригонометрических функций.
1. Замена t =sin x (t =cos x). Эта замена используется в случае, когда подынтегральная функция – произведение нечетной степени косинуса (синуса) и функции, зависящей только от синуса (косинуса).
 =
=  =
=  =
=  = –
= –  = –
= –  +2
+2  = – t +2arctg t +C = –sin x +2arctg(sin x)+C.
= – t +2arctg t +C = –sin x +2arctg(sin x)+C.
 =
=  =
=  = –
= – 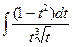
= –  +
+ 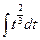 =
= 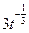 +
+  +С=
+С=  +
+  +C.
+C.
2. Использование формул понижения степени: 2сos2 x =1+cos2 x, 2sin2 x =1–cos2 x. Эти формулы полезны, например, в тех случаях, когда подынтегральная функция – произведение четных степеней синуса и косинуса.
 =
=  =
=
=  =
= 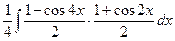 =
=
=  =
=
=  =
=
= 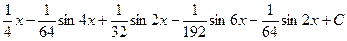 =
=
=  .
.
3. Замена t =tg x ( t =ctg t). Эта замена также может использоваться в тех случаях, когда подынтегральная функция – произведение (или частное) четных степеней синуса и косинуса.
 =
= 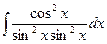 =
=  = –
= –  = –
= –  + С = –
+ С = –  +С.
+С.
Эта же замена удобна для интегрирования степеней тангенса или котангенса.
 =
=  =
=  =
=  =
=  –
–
–  =
=  –
–  =
=  –
–  =
=
=  –
–  +
+  =
=  –
–  +
+  =
=  –
–
–  +
+  =
=  –
–  +
+  –
–  =
=
=  –
–  +
+  +
+  =
=  –
– 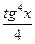 +
+  +lnï cos x ï +C.
+lnï cos x ï +C.
 =
=  =
=  =
=  =
=
= –  –
–  = –
= –  –
–  = –
= –  –
–
–  =–
=–  +
+  +
+ 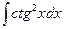 = –
= –  +
+
+  +
+  = –
= –  +
+  –ctg x – x +C= –
–ctg x – x +C= –  +
+
+  –ctg x – x +C.
–ctg x – x +C.
4. Универсальная тригонометрическая замена. Так называют подстановку t =tg  . При этом sin x =
. При этом sin x =  , cos x =
, cos x =  , dx =
, dx =  .
.
 =
=  =
=
= 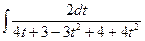 =
=  =
=  =
=
=  +C=
+C= 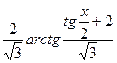 +C.
+C.
3.3. Интегрирование иррациональных функций
Покажем на примерах некоторые способы интегрирования иррациональных функций.
1. Чтобы проинтегрировать рациональную функцию, зависящую от х и от нескольких дробных степеней двучлена:  ,...,
,...,  , – используют замену t =
, – используют замену t =  (n – наименьшее общее кратное чисел n1, …, nk).
(n – наименьшее общее кратное чисел n1, …, nk).
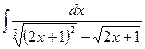 =
=  =
=  =
=  =
= 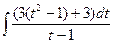 =3
=3  +3
+3  =
=  +3 t +3lnï t –1ï +C=
+3 t +3lnï t –1ï +C=  +3
+3  +3lnï
+3lnï  –1ï +C.
–1ï +C.
2. Интеграл вида  сводится к одному из табличных интегралов:
сводится к одному из табличных интегралов:  или
или 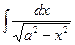 .
.
 =
= 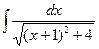 =
= 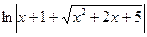 +С.
+С.
 =
=  =
=
=  =
=  =
=  arcsin
arcsin  +C=
+C=
=  arcsin
arcsin  +C.
+C.
3. Интеграл вида  сводится к интегралу из предыдущего пункта следующим образом. Сначала числитель дроби записывается в виде a(d (ax 2+ bx + c))+b dx; тогда
сводится к интегралу из предыдущего пункта следующим образом. Сначала числитель дроби записывается в виде a(d (ax 2+ bx + c))+b dx; тогда  =a
=a  +b
+b  =
=
=2a  +b
+b  .
.
 =
= 
 –13
–13  =
=
= 
 –13
–13  =
= 
 – –
– – 
 +С.
+С.
 = –
= – 
 +13
+13  =
=
= –3  +13
+13  = –3
= –3  +
+
+13arcsin(x –3)+C.
4. Интеграл вида 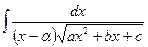 берется с помощью замены t =
берется с помощью замены t = 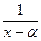 .
.
 =
=  =
=  =
= 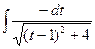
= –  +С=.–
+С=.–  +C.
+C.
 =
=  =
=  =
=
=  =
=  =
= 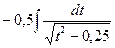 =
=
= –0, 5  +С=.–0, 5
+С=.–0, 5  +C.
+C.

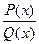 , где P(x) и Q(x) – многочлены. Если степень числителя меньше степени знаменателя, то дробь называется правильной; в противном случае – неправильной. Всякая правильная дробь может быть представлена в виде суммы простейших дробей; так называют дроби четырех типов:
, где P(x) и Q(x) – многочлены. Если степень числителя меньше степени знаменателя, то дробь называется правильной; в противном случае – неправильной. Всякая правильная дробь может быть представлена в виде суммы простейших дробей; так называют дроби четырех типов:  ;
; , где n – натуральное число, не равное единице;
, где n – натуральное число, не равное единице;  ;
;  , где n – натуральное число, не равное единице. Здесь А, В, а, p, q – числа; квадратные трехчлены x 2+ px + q не имеют действительных корней. Для того, чтобы представить правильную дробь
, где n – натуральное число, не равное единице. Здесь А, В, а, p, q – числа; квадратные трехчлены x 2+ px + q не имеют действительных корней. Для того, чтобы представить правильную дробь  +С. Способы интегрирования дробей третьего и четвертого типа будут показаны на примерах.
+С. Способы интегрирования дробей третьего и четвертого типа будут показаны на примерах. . Разложим знаменатель на множители: х 4–4 х 3+4 х 2= х 2(х 2–4 х +4)= х 2(х –2)2. Значит, разложение дроби в сумму простейших содержит две дроби первого и две дроби второго типа:
. Разложим знаменатель на множители: х 4–4 х 3+4 х 2= х 2(х 2–4 х +4)= х 2(х –2)2. Значит, разложение дроби в сумму простейших содержит две дроби первого и две дроби второго типа:  +
+  +
+  +
+  . Приведем дроби в правой части к общему знаменателю и приравняем числители правой и левой части: х 3–2 х 2–3 х +4=А х (х –2)2+В(х –2)2+С х 2(х –2)+D х 2. Это равенство должно выполняться при всех значениях х. Подставив четыре различных значения х, получим уравнения, связывающие коэффициенты. При х =0: 4=4В; при х =2: –2=4D; при х =1: 0=А+В–С+D; при х = –1: 4= –9А+9В–3С+D. Отсюда В=1, D= –0, 5, А=0, 25, С=0, 75. Значит,
. Приведем дроби в правой части к общему знаменателю и приравняем числители правой и левой части: х 3–2 х 2–3 х +4=А х (х –2)2+В(х –2)2+С х 2(х –2)+D х 2. Это равенство должно выполняться при всех значениях х. Подставив четыре различных значения х, получим уравнения, связывающие коэффициенты. При х =0: 4=4В; при х =2: –2=4D; при х =1: 0=А+В–С+D; при х = –1: 4= –9А+9В–3С+D. Отсюда В=1, D= –0, 5, А=0, 25, С=0, 75. Значит,  +
+  +
+  –
–  . А тогда ò
. А тогда ò  +0, 75lnï x –2ï +
+0, 75lnï x –2ï +  +C.
+C. . Представим ее в виде (2 х –1)+
. Представим ее в виде (2 х –1)+  . Полученная правильная дробь – простейшая дробь третьего типа. Найдем производную ее знаменателя: (х 2–6 х +11)¢ =2 х –6. Теперь запишем числитель дроби в виде А(2 х –6)+В, получим: х –9=0, 5(2 х –6)–6, т.е. ò
. Полученная правильная дробь – простейшая дробь третьего типа. Найдем производную ее знаменателя: (х 2–6 х +11)¢ =2 х –6. Теперь запишем числитель дроби в виде А(2 х –6)+В, получим: х –9=0, 5(2 х –6)–6, т.е. ò  dx =0, 5ò
dx =0, 5ò  –6ò
–6ò 
 –6ò
–6ò  =
= arctg
arctg  +C.
+C.
 =
=  =
=  =
=  = –
= –  = –
= –  +2
+2  = – t +2arctg t +C = –sin x +2arctg(sin x)+C.
= – t +2arctg t +C = –sin x +2arctg(sin x)+C. =
=  =
=  = –
= – 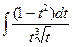
 +
+ 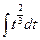 =
= 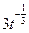 +
+  +С=
+С=  +
+  +C.
+C. =
=  =
= =
= 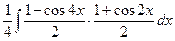 =
= =
= =
=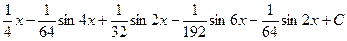 =
= .
. =
= 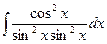 =
=  = –
= –  = –
= –  + С = –
+ С = –  +С.
+С. =
=  =
=  =
=  =
=  –
– =
=  =
=  =
= +
+  =
=  =
=  =
=  –
–  =
= –
–  +
+  +
+  =
=  –
– 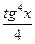 +
+  +lnï cos x ï +C.
+lnï cos x ï +C. =
=  =
=  =
=  =
= –
–  = –
= –  = –
= –  =–
=–  +
+ 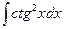 = –
= –  = –
= –  +
+  +
+ . При этом sin x =
. При этом sin x =  , cos x =
, cos x =  , dx =
, dx =  .
. =
=  =
=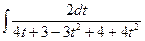 =
=  =
=  =
= +C=
+C= 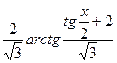 +C.
+C. ,...,
,...,  , – используют замену t =
, – используют замену t =  (n – наименьшее общее кратное чисел n1, …, nk).
(n – наименьшее общее кратное чисел n1, …, nk).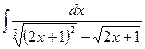 =
=  =
=  =
=  =
= 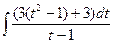 =3
=3  +3
+3  =
=  +3 t +3lnï t –1ï +C=
+3 t +3lnï t –1ï +C=  +3
+3  +3lnï
+3lnï  сводится к одному из табличных интегралов:
сводится к одному из табличных интегралов:  или
или 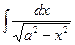 .
. =
= 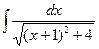 =
= 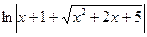 +С.
+С. =
=  =
= =
=  =
=  arcsin
arcsin  +C=
+C= +C.
+C. сводится к интегралу из предыдущего пункта следующим образом. Сначала числитель дроби записывается в виде a(d (ax 2+ bx + c))+b dx; тогда
сводится к интегралу из предыдущего пункта следующим образом. Сначала числитель дроби записывается в виде a(d (ax 2+ bx + c))+b dx; тогда  +b
+b  +b
+b  =
= 
 –13
–13  =
=
 –13
–13  =
= 
 +С.
+С. = –
= – 
 +13
+13  =
= +13
+13  = –3
= –3 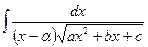 берется с помощью замены t =
берется с помощью замены t = 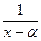 .
. =
=  =
=  =
= 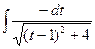
 +С=.–
+С=.–  +C.
+C. =
=  =
=  =
= =
=  =
= 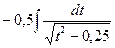 =
= +С=.–0, 5
+С=.–0, 5  +C.
+C.


