Предел и непрерывность
Раздел V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ Основные понятия Пусть DÍ R n. Отображение f: D® R будемназывать функцией n переменных. Если (х 1, х 2,..., х n) – элемент множества D, то его образ f (х 1, х 2,..., х n) – действительное число. Множество D – область определения функции f. Переменные х 1, х 2,..., х n называют аргументами этой функции. Примеры. 1) Формула равномерного движения S=vt задает пройденный путь как функцию двух переменных – скорости и времени: S= f (v, t). 2) Закон Ома V=IR задает напряжение как функцию двух переменных – силы тока и сопротивления: V= f (I, R). 3) Формула объема прямоугольного параллелепипеда V= abc задает объем как функцию трех переменных – длины, ширины и высоты: V= f (a, b, c). · Если f (x, y) – функция двух переменных, то область определения D(f) – часть плоскости. Примеры. 1) Пусть f (x, y)= 2) Пусть f (x, y)= 3) Пусть f (x, y)=ln(x 2+ y 2–1). Тогда D(f) состоит из всех точек (x, y), для которых х 2+ у 2–1> 0. Эти точки составляют всю плоскость, кроме круга с центром в начале координат и радиусом 1. Таким образом, D(f) – вся плоскость без этого круга. · Если f (x, y) – функция двух переменных, то поверхность z = f (x, y) называют графиком этой функции, а линии на плоскости, заданные уравнениями вида f (x, y)=С, называют линиями уровня. Примеры. 1) Пусть f (x, y)= 2) Пусть f (x, y)= х 2+ у 2–1. Область определения этой функции – вся плоскость. График функции – поверхность z = х 2+ у 2–1, то есть параболоид вращения с вершиной в точке (0; 0; –1) и осью вращения O z. Линии уровня х 2+ у 2–1=С, если C> –1, – это окружности с центром в начале координат и радиусом
Предел и непрерывность Пусть Определение 1. Функция f нескольких переменных, определенная в некоторой проколотой окрестности точки Свойства бесконечно малых функций нескольких переменных аналогичны свойствам бесконечно малых функций одной переменной. Попробуйте сформулировать их самостоятельно. Определение 2. Число b называется пределом функции f ( В частности, если функция f ( Примеры. 1) Пусть f ( 2) Пусть f ( Свойства предела функции нескольких переменных аналогичны свойствам предела функции одной переменной. Сформулируем их в виде теорем, которые примем без доказательства. Теорема 1 (о единственности предела). Если
Теорема 2 (об ограниченности функции, имеющей предел). Если функция имеет предел при Теорема 3 (о переходе к пределу в неравенстве). Если Следствие. Если Теорема 4 (о промежуточной функции). Если Теорема 5 (об арифметических операциях). 1) Если 2) Если Следствие. Если 3) Если Следствие. Если Примеры. Обозначим 1) 2) 3) Покажем, что 4) Для вычисления Определение 3. Функция f ( Перечислим свойства непрерывных функций нескольких переменных. Теорема 6 (о локальной ограниченности). Если функция непрерывна в точке, то она ограничена в некоторой окрестности этой точки. Теорема 7 (о сохранении знака). Если функция f ( Теорема 8 (об арифметических операциях). Если функции f ( Теорема 9 (о непрерывности сложной функции двух переменных). Пусть функции u (x, y) и v (x, y) непрерывны в точке (х о, у о), а функция f (u, v) непрерывна в точке (u o, v o), где u o= u (x о, y о), v o= v (x о, y о). Тогда функция f (u (x, y), v (x, y)) непрерывна в точке (х о, у о). Замечание 1. Рассмотрим функцию двух переменных f (x, y). Рассмотрим точки (x 0, y 0) и (x 0+D x, y 0+D y). Разность f (x 0+D x, y 0+D y)– f (x 0, y 0) обозначим D f и будем называть приращением функции в точке (x 0, y 0). При фиксированной точке (x 0, y 0) приращение будет функцией от D x и D y (то есть от приращений аргументов). Из определения непрерывности следует, что функция f (x, y) непрерывна в точке (x 0, y 0) тогда и только тогда, когда в этой точке Пример. Пусть f (x, y)= Замечание 2. Кроме приращения D f, для функции двух переменных рассматривают так называемые частные приращения по х и по у: D хf = f (x 0+D x, y 0)– f (x 0, y 0) и D уf = f (x 0, y 0+D y)– f (x 0, y 0). Первое из них является функцией только от D x, а второе – только от D y. Аналогично можно определить частные приращения и для функции любого числа переменных.
|

 . Тогда D(f) состоит из всех точек (x, y), для которых 4– х 2– у 2³ 0. Эти точки составляют круг с центром в начале координат и радиусом 2. Таким образом, D(f) – круг.
. Тогда D(f) состоит из всех точек (x, y), для которых 4– х 2– у 2³ 0. Эти точки составляют круг с центром в начале координат и радиусом 2. Таким образом, D(f) – круг.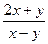 . Тогда D(f) состоит из всех точек (x, y), для которых х – у ¹ 0. Эти точки составляют всю плоскость, кроме прямой х = у. Таким образом, D(f) – вся плоскость без этой прямой.
. Тогда D(f) состоит из всех точек (x, y), для которых х – у ¹ 0. Эти точки составляют всю плоскость, кроме прямой х = у. Таким образом, D(f) – вся плоскость без этой прямой. . Если С=2, то линия уровня состоит из одной точки – начала координат. При С< 0 или С> 2 линии уровня не существуют.
. Если С=2, то линия уровня состоит из одной точки – начала координат. При С< 0 или С> 2 линии уровня не существуют.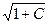 . Если С=–1, то линия уровня состоит из одной точки – начала координат. При С< –1линии уровня не существуют.·
. Если С=–1, то линия уровня состоит из одной точки – начала координат. При С< –1линии уровня не существуют.·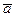 Î R n:
Î R n:  Î R n, для которых ç
Î R n, для которых ç  , стремящемся к
, стремящемся к  .
.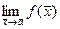 =0.
=0. =С.
=С.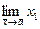 = a 1. ·
= a 1. · = с, причем f (
= с, причем f (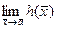 = b.
= b.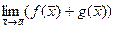 = b + c.
= b + c.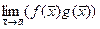 = bc.
= bc.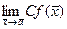 = Cb.
= Cb. =
= 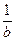 .
.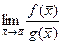 =
= 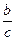 .
.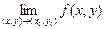 через
через  .
. =
=  = 5.
= 5. =
=  =
=  . Мы воспользовались здесь эквивалентностями: ln(1+a)~a и sina~a при a®0.
. Мы воспользовались здесь эквивалентностями: ln(1+a)~a и sina~a при a®0.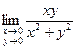 не существует. Предположим сначала, что точка (x, y) приближается к точке (0; 0) по прямой y = x. Тогда
не существует. Предположим сначала, что точка (x, y) приближается к точке (0; 0) по прямой y = x. Тогда  =
=  . Если же прямую y = x заменить прямой y = – x, то получим
. Если же прямую y = x заменить прямой y = – x, то получим  = –
= – 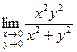 воспользуемся полярными координатами: пусть х =rcosj, y =rsinj. Тогда
воспользуемся полярными координатами: пусть х =rcosj, y =rsinj. Тогда  =
=  r2cos2jsin2j; 0£ r2cos2jsin2j£ r2 при любом j;
r2cos2jsin2j; 0£ r2cos2jsin2j£ r2 при любом j;  непрерывна в точке
непрерывна в точке  =0 (то есть приращение функции в этой точке является бесконечно малой при D x ®0 и D y ®0).
=0 (то есть приращение функции в этой точке является бесконечно малой при D x ®0 и D y ®0). . Тогда приращение функции в точке (0; 0) имеет вид: D f =
. Тогда приращение функции в точке (0; 0) имеет вид: D f =  . Как показано в примере выше, при D x ®0 и D y ®0 эта функция не имеет предела. Значит, функция f (x, y) не является непрерывной в точке (0; 0).·
. Как показано в примере выше, при D x ®0 и D y ®0 эта функция не имеет предела. Значит, функция f (x, y) не является непрерывной в точке (0; 0).·


