Определенный интеграл
4.1.Площадь криволинейной трапеции. Масса неоднородного стержня Рассмотрим криволинейную трапецию, ограниченную линиями: x = a, x = b, y = f (x), y =0, где a < b, f (x)³ 0. Чтобы найти площадь криволинейной трапеции, разделим отрезок [ a; b ] на n равных частей, в каждом маленьком отрезке выберем точку и построим на нем прямоугольник, высота которого равна значению f (x) в выбранной точке. Если площадь полученной ступенчатой фигуры при увеличении числа n стремится к некоторому числу S, то S естественно считать площадью криволинейной трапеции. Пример. Пусть криволинейная трапеция ограничена линиями: x =0, x =1, y = x 2. Разделим отрезок [0; 1] на n равных частей. На каждом отрезке [ Аналогично можно определить массу тонкого стержня переменной линейной плотности: стержень делится на отрезки, в каждом из которых выбирается некоторая точка. Тогда масса стержня приближенно равна сумме произведений вида r(xk)D xk, где r(xk) – значение плотности в выбранной точке, а D xk – длина соответствующего отрезка. Если при неограниченном увеличении числа отрезков эта сумма стремится к некоторому числу М, то М считают массой стержня. 4.2.Определение определенного интеграла Пусть функция f (x) ограничена на отрезке [ a; b ]. Рассмотрим разбиение отрезка: a = x 0< x 1< …< x n–1< x n= b. На каждом промежутке [ xk –1; xk ], где 1£ k £ n, выберем точку x k. Обозначим D xk = xk – xk –1. Диаметром разбиения назовем число d= Определение. Функция f (x) называется интегрируемой на отрезке [ a; b ], если при d®0 существует предел интегральных сумм, не зависящий от разбиения. Значение этого предела называется определенным интегралом функции f (x) на отрезке [ a; b ] и обозначается Замечание. Приведенные в пункте 4.1 примеры характеризуют геометрический и физический смысл определенного интеграла: если f (x)³ 0 на отрезке [ a; b ], то 4.3.Основные теоремы об определенном интеграле
Следующие две теоремы примем без доказательства. Теорема 1. Если функция f (x) непрерывна на отрезке [ a; b ], то она интегрируема на этом отрезке. Теорема 2. Если функция f (x) интегрируема на отрезке [ a; c ] и на отрезке [ c; b ], где a < c < b, то f (x) интегрируема на отрезке [ a; b ], причем Равенство Теорема 3 (о среднем значении). Если функция f (x) непрерывна на отрезке [ a; b ], то на этом отрезке существует такое число с, что Доказательство. Пусть m и М – соответственно наименьшее и наибольшее значение функции на отрезке. Тогда для всякой интегральной суммы S= Значение f (с) называется в этом случае средним значением функции f (х) на отрезке [ a; b ]. Геометрически теорема 3 означает, что если f (x)³ 0 на отрезке [ a; b ], то площадь криволинейной трапеции, ограниченной линиями x = a, x = b, y = f (x), y =0, равна площади прямоугольника, построенного на этом отрезке и имеющего высоту, равную значению функции в некоторой точке отрезка.
|

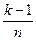 ;
;  ], где 1£ k £ n, построим прямоугольник, высота которого равна
], где 1£ k £ n, построим прямоугольник, высота которого равна 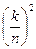 (значению функции в правом конце отрезка). Тогда площадь полученной ступенчатой фигуры равна
(значению функции в правом конце отрезка). Тогда площадь полученной ступенчатой фигуры равна  , или
, или  . Используя формулу суммы квадратов первых n натуральных чисел, получим выражение
. Используя формулу суммы квадратов первых n натуральных чисел, получим выражение  =
=  . При n®¥ предел этого выражения равен
. При n®¥ предел этого выражения равен 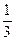 . Это число считают площадью криволинейной данной трапеции.·
. Это число считают площадью криволинейной данной трапеции.· и рассмотрим сумму f (x 1)D x 1+ f (x 2)D x 2+…+ f (x n)D x n; ее называют интегральной суммой данного разбиения.
и рассмотрим сумму f (x 1)D x 1+ f (x 2)D x 2+…+ f (x n)D x n; ее называют интегральной суммой данного разбиения. .
. .
.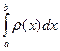 –масса этого стержня.
–масса этого стержня. =
=  +
+  .
. справедливо неравенство:
справедливо неравенство:  £ S£
£ S£  , – то есть m(b – a)£ S£ M(b – a). А значит, m(b – a)£
, – то есть m(b – a)£ S£ M(b – a). А значит, m(b – a)£  заключено между наименьшим значением m и наибольшим значением M функции f (x). По теореме о промежуточном значении непрерывной на отрезке функции существует c Î [ a; b ]: f (с)=
заключено между наименьшим значением m и наибольшим значением M функции f (x). По теореме о промежуточном значении непрерывной на отрезке функции существует c Î [ a; b ]: f (с)= 


