Неопределенный интеграл. ?казательство. Поскольку (F(x)+С)¢=F¢(x)=f(x), то любая функция вида F(x)+С – первообразная функции f(x). ?казательство. Поскольку (F(x)+С)¢=F¢(x)=f(x), то любая функция вида F(x)+С – первообразная функции f(x)
1.1.Первообразная и неопределенный интеграл Определение 1. Функция F(x) называется первообразной функции f (x) на отрезке [ a; b ], если на этом отрезке f (x)= F¢ (x). Примеры. 1)Поскольку 2)Поскольку 3)Поскольку Теорема 1. Если функция f (x) имеет на отрезке [ a; b ] первообразную F(x), то она имеет на этом отрезке бесконечно много первообразных, причем любую из них можно записать в виде F(x)+С, где С – произвольная константа. Доказательство. Поскольку (F(x)+С)¢ =F¢ (x)= f (x), то любая функция вида F(x)+С – первообразная функции f (x). С другой стороны, если какая-нибудь функция G(x) – первообразная функции f (x), то F¢ (x)=G¢ (x) на отрезке [ a; b ]. А тогда эти функции отличаются на константу: G(x)=F(x)+С. Теорема доказана. Определение 2. Множество всех первообразных функции f (x) на данном отрезке называется неопределенным интегралом этой функции и обозначается ò f (x) dx. Если F(x) – одна из первообразных функции f (x), то пишут ò f (x) dx = F(x)+С. Из определения сразу получаются два свойства неопределенного интеграла. Теорема 2. d (ò f (x) dx)= f (x) dx. Доказательство. Пусть ò f (x) dx = F(x)+С. Тогда d (ò f (x) dx)= d (F(x)+С)= F¢ (x) dx = f (x) dx, ч.т.д. Теорема 3. ò dF (x) = F(x)+С. Доказательство. ò dF (x)=ò F¢ (x) dx. Поскольку(F(x)+С)¢ = F¢ (x), то ò dF (x)= F(x)+С, ч.т.д. 1.2. Таблица неопределенных интегралов. Свойство линейности Используя таблицу производных, составим следующую таблицу неопределенных интегралов.
Примеры. 1) 2) Вычислим 3) Вычислим 4) Вычислим 5) Вычислим Следующее свойство неопределенного интеграла позволяет вычислять интегралы от линейных комбинаций табличных функций. Свойство линейности. Если a, b – числа, f (x) и g (x) – функции, имеющие первообразные, то ò (a f (x)+b g (x)) dx = aò f (x) dx +bò g (x) dx. Чтобы убедиться в справедливости этого равенства, достаточно продифференцировать правую часть. Примеры. 1)Свойство линейности позволяет записать
2) +
|

 = х 3 при любом х, то функция
= х 3 при любом х, то функция  – первообразная функции х 3 на всей числовой прямой.
– первообразная функции х 3 на всей числовой прямой. =sin3 х при любом х, то функция
=sin3 х при любом х, то функция 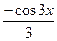 – первообразная функции sin3 х на всей числовой прямой.
– первообразная функции sin3 х на всей числовой прямой. =
=  при х > 0, то функция ln x – первообразная функции
при х > 0, то функция ln x – первообразная функции 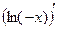 =
=  = х +С
= х +С
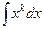 =
=  +С,
k ¹ –1
+С,
k ¹ –1
 = lnï x ï +С
= lnï x ï +С
 =
= 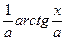 +C
+C
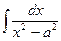 =
=  +C
+C
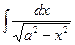 =
=  +C
+C
 =
=  +C
+C
 = –cos х +С
= –cos х +С
 = sin х +С
= sin х +С
 =tg x +C
=tg x +C
 = –ctg x +C
= –ctg x +C
 =
=  +C
+C
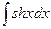 =ch x +C
=ch x +C
 =sh x +C
=sh x +C
 =th x +C
=th x +C
 = –cth x +C
= –cth x +C
 =
=  . Используем формулу (2) для k = –
. Используем формулу (2) для k = – 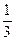 :
:  +С=
+С=  +С.
+С. . Используем формулу (4) для а =4:
. Используем формулу (4) для а =4: 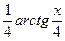 +C.
+C. . Используем формулу (5) для а =4:
. Используем формулу (5) для а =4:  +C =
+C =  +С.
+С. . Используем формулу (6) для а =
. Используем формулу (6) для а =  :
:  +C.
+C. . Используем формулу (7) для а =
. Используем формулу (7) для а = 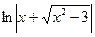 +C. ·
+C. · в виде
в виде  +
+  –5
–5  =
= –5
–5  = lnï x ï +
= lnï x ï +  –5
–5  +С= lnï x ï +2
+С= lnï x ï +2  +
+  +С.
+С. =
=  =
= 
 =
=  =tg x –ctg x +C.·
=tg x –ctg x +C.·


