Дифференциальное исчисление
функций двух переменных 3.1. Дифференцируемость функции в точке Определение 1. Функция двух переменных f (x, у), определенная в некоторой окрестности точки (х 0, у 0), называется дифференцируемой в этой точке, если приращение функции в этой точке можно представить в виде: D f = AD x +ВD у +a(D x, D у)D x +b(D x, D у)D у, где А и В – числа, а a(D x, D у) и b(D x, D у) – бесконечно малые при D x ®0 и D у ®0. Главную линейную часть этого выражения – сумму AD x +ВD у – называют дифференциалом функции f (x, у) в точке (х 0, у 0) и обозначают d f. Из этого определения следует, что если функция f (x, у) дифференцируема в точке (х 0, у 0), то в этой точке
Определение 2. Пусть функция f (x, у) определена в некоторой окрестности точки (х 0, у 0). Если в этой точке существует Итак, справедлива следующая теорема. Теорема 1 (необходимое условие дифференцируемости функции в точке). Если функция f (x, у) дифференцируема в точке (х 0, у 0), то в этой точке существуют частные производные Замечание. Значит, d f = Теорема 2 (непрерывность дифференцируемой функции). Если функция f (x, у) дифференцируема в точке (х 0, у 0), то она непрерывна в этой точке. Доказательство. Поскольку для дифференцируемой функции D f =AD x +ВD у +a(D x, D у)D x +b(D x, D у)D у, где А и В – числа, а a(D x, D у) и b(D x, D у) – бесконечно малые при D x ®0 и D у ®0, то D f является бесконечно малой при D x ®0 и D у ®0. А значит, согласно замечанию 1 из предыдущего пункта, функция f (x, у) непрерывна в точке (х 0, у 0), ч.т.д. Примеры. 1)Пусть f (x, у) = 2)Пусть f (x, у) = х 3 у +sin(x 2+ 2 x cos(x 2+ 3)Пусть f (x, у)=
4)Пусть 5)Уравнение F(x, y)=0 неявно задает у как функцию х. Пусть функция F дифференцируема; будем для краткости обозначать 3.2. Достаточное условие дифференцируемости Пример. Пусть f (x, y)= Теорема 3 (достаточное условие дифференцируемости функции в точке). Если функция f (x, у) имеет в точке (х 0, у 0) непрерывные частные производные, то она дифференцируема в этой точке. Доказательство. D f = f (x 0+D x, y 0+D y)– f (x 0, y 0)= (f (x 0+D x, y 0+D y)– f (x 0+D x, y 0))+(f (x 0+D x, y 0) –f (x 0, y 0)). Пусть u (y) = f (x 0+D x, y), v (x)= f (x, y 0). Тогда u ¢ (y)= fy (x 0+D x, y), v ¢ (x)= fx (x, y 0). Применив к этим функциям теорему Лагранжа, получим: D f = fy (x 0+D x, с 1)D y + fx (с 2, y 0)D х, с 1 лежит между y 0 и y 0+D y, а с 2 – между х 0 и х 0+D х. Поскольку fy и fх непрерывны в точке (х 0, у 0), то fy (x 0+D x, с 1)= fy (x 0, у 0)+b(D x, D y) и fx (с 2, y 0)= fх (x 0, у 0)+ a(D x, D y), где a(D x, D y) и b(D x, D y) – бесконечно малые при D x ®0 и D y ®0. Значит, D f =(fy (x 0, у 0)+b(D x, D y))D y + (fх (x 0, у 0)+ a(D x, D y))D х = fх (x 0, у 0)D х + fy (x 0, у 0)D y +a(D x, D y)D х +b(D x, D y)D y, то есть f (x, у) дифференцируема в точке (х 0, у 0), ч.т.д. 3.3. Применение дифференциала 1о. Так же, как для функции одной переменной, дифференциал функции двух переменных можно использовать для приближенных вычислений: f (х 0+D x, у 0+D у)» f (х 0, у 0) + Пример. Найдем приближенно D у = –0, 02, f (x 0, у 0) = 2о. Рассмотрим поверхность z = f (x, y), где функция f (x, y) дифференцируема в некоторой окрестности точки (х 0, у 0). Можно доказать (мы этого делать не будем), что уравнение касательной плоскости к поверхности в точке (х 0, у 0, z 0), где z 0= f (х 0, у 0), имеет вид: z – z 0= fх¢ (х 0, у 0)(x – x 0)+ fу¢ (х 0, у 0)(у – у 0). Таким образом, нормальный вектор касательной плоскости имеет координаты (fх¢ (х 0, у 0); fу¢ (х 0, у 0); –1). Отсюда получаем уравнение нормали к поверхности в точке (х 0, у 0, z 0), где z 0= f (х 0, у 0):
Замечание. Если поверхность задана уравнением F(x, y, z)=0, причем функция F(x, y, z) дифференцируема в некоторой окрестности точки (х 0, у 0, z 0), то уравнения касательной плоскости и нормали в этой точке приобретают вид: F х¢ (х 0, у 0, z 0)(x – x 0)+F у¢ (х 0, у 0, z 0)(у – у 0)+F z¢ (х 0, у 0, z 0)(z – z 0)=0;
Пример. Составим уравнение касательной плоскости и нормали к сфере x 2+ y 2+ z 2–16=0 в точке (2, 2, 2 4(x –2)+4(y –2)+4 Уравнение нормали: 3.4. Дифференцирование сложной функции Следующую теорему примем без доказательства. Теорема 4 (о дифференцировании сложной функции). Пусть функции u = u (x, y) и v = v (x, y) имеют непрерывные частные производные в некоторой окрестности точки (х 0, у 0), а функция z = f (u, v) – в некоторой окрестности точки (u 0, v 0), где u o= u (x о, y о), v o= v (x о, y о). Тогда сложная функция z (x, y)= f (u (x, y), v (x, y)) дифференцируема в точке (х 0, у 0), причем Примеры. 1) Пусть z = u 2+ v 3, u = 2) Пусть z =ln t, t =sin x +cos y. Тогда по формулам теоремы 4 получаем:
3.5. Производная по направлению. Градиент Определение 3. Пусть функция z = f (x, y) определена в некоторой окрестности точки Р0(х 0, у 0), l – луч с началом в точке Р0, точка Р(х, у) принадлежит l. Длину отрезка Р0Р обозначим D l, разность f (x, y)– f (х 0, у 0) обозначим D f. Если существует Замечание. Частные производные Теорема 5. Если функция z = f (x, y) имеет в некоторой окрестности точки (х 0, у 0) непрерывные частные производные, то в этой точке функция имеет производную по любому направлению, причем Доказательство. Запишем D f в виде f (x 0+D х, у 0+D у)– f (x 0, у 0+D у)+ f (x 0, у 0+D у)– f (х 0, у 0)=D хf (x 0, у 0+D у)+D уf (x 0, у 0). Тогда =
рывность частной производной Определение 4. Если функция z = f (x, y) имеет в точке (х 0, у 0) частные производные, то градиентом функции в этой точке называется вектор grad f =( Замечание. Пусть 3.6. Частные производные высших порядков Определение 5. Пусть функция z = f (x, y) имеет в некоторой окрестности точки (х 0, у 0) частные производные Частных производных второго порядка существует, вообще говоря, четыре:
Аналогично определяются частные производные третьего, четвертого и других порядков. Пример. 1) Для функции f (x, y)= x 2 y 3 найдем 2) Для функции f (x, y)=sin(x 2+ y 3) найдем
В рассмотренном примере смешанные частные производные второго порядка Теорема 6. Если функция f (x, y) имеет в некоторой точке непрерывные частные производные второго порядка, то в этой точке
|

 =А+a(D x, 0) и
=А+a(D x, 0) и  =В+b(0, D у). Тогда существуют пределы:
=В+b(0, D у). Тогда существуют пределы:  = А и
= А и  = В.
= В. . Аналогично
. Аналогично  – частная производная по у. Таким же образом определяются частные производные для функции любого числа переменных.
– частная производная по у. Таким же образом определяются частные производные для функции любого числа переменных. . Эта функция непрерывна на всей плоскости и, в частности, в точке (0; 0). Приращение D хf в этой точке равно
. Эта функция непрерывна на всей плоскости и, в частности, в точке (0; 0). Приращение D хf в этой точке равно  , то есть ï D x ï. Поэтому отношение D хf к D x равно 1 или –1 в зависимости от знака D x, и предел этого отношения при D x ®0 не существует. Отсутствие частной производной по х означает, что функция не дифференцируема в точке (0; 0). Таким образом, непрерывность является необходимым, но не достаточным условием дифференцируемости.
, то есть ï D x ï. Поэтому отношение D хf к D x равно 1 или –1 в зависимости от знака D x, и предел этого отношения при D x ®0 не существует. Отсутствие частной производной по х означает, что функция не дифференцируема в точке (0; 0). Таким образом, непрерывность является необходимым, но не достаточным условием дифференцируемости. )+tg x +ln y. Найдем частные производные этой функции. Поскольку при вычислении частной производной по одному из аргументов другой аргумент не меняется, то достаточно найти обычную производную, считая второй аргумент константой. Тогда получим:
)+tg x +ln y. Найдем частные производные этой функции. Поскольку при вычислении частной производной по одному из аргументов другой аргумент не меняется, то достаточно найти обычную производную, считая второй аргумент константой. Тогда получим:  +0 =3 x 2 у +
+0 =3 x 2 у + +
+  .
. . Найдем дифференциал этой функции в точке (2; 1), если d x =0, 1, d y = –0, 2. Имеем:
. Найдем дифференциал этой функции в точке (2; 1), если d x =0, 1, d y = –0, 2. Имеем:  . Значит, в данной точке
. Значит, в данной точке  ,
,  , поэтому 2 х 6 у +
, поэтому 2 х 6 у + 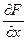 и
и  соответственно F x и F y. Можно показать, что если F y ¹ 0, то функция у (х) дифференцируема и
соответственно F x и F y. Можно показать, что если F y ¹ 0, то функция у (х) дифференцируема и  . Например, для функции у (х), неявно заданной уравнением cos(x + y)+ y =0,
. Например, для функции у (х), неявно заданной уравнением cos(x + y)+ y =0,  =
=  . Точно так же уравнение F(x, y, z)=0 неявно задает z как функцию х и у. Можно показать, что если функция F дифференцируема, причем F z ¹ 0, то функция z (х, y) дифференцируема, zx =
. Точно так же уравнение F(x, y, z)=0 неявно задает z как функцию х и у. Можно показать, что если функция F дифференцируема, причем F z ¹ 0, то функция z (х, y) дифференцируема, zx =  и zу =
и zу =  . Например, для функции z (х, y), неявно заданной уравнением x + y + z – xyz =0, zx =
. Например, для функции z (х, y), неявно заданной уравнением x + y + z – xyz =0, zx =  и zу =
и zу =  . ·
. · . Как было показано выше, эта функция не является непрерывной в точке (0; 0), а следовательно, не дифференцируема в этой точке. С другой стороны, частные приращения функции в точке (0; 0) равны нулю, а значит, обе частные производные равны нулю. Таким образом, существование частных производных не является достаточным условием дифференцируемости. ·
. Как было показано выше, эта функция не является непрерывной в точке (0; 0), а следовательно, не дифференцируема в этой точке. С другой стороны, частные приращения функции в точке (0; 0) равны нулю, а значит, обе частные производные равны нулю. Таким образом, существование частных производных не является достаточным условием дифференцируемости. · D x +
D x +  D у. (*)
D у. (*) . Это число является значением функции f (x, у)=
. Это число является значением функции f (x, у)=  при х =1, 03, у =1, 98. Поскольку 1, 03=1+0, 03, 1, 98=2–0, 02, то
при х =1, 03, у =1, 98. Поскольку 1, 03=1+0, 03, 1, 98=2–0, 02, то  =3. Так как fх¢ (х, у)=
=3. Так как fх¢ (х, у)=  и fу¢ (х, у)=
и fу¢ (х, у)= 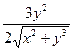 , то fх¢ (х 0, у 0)=
, то fх¢ (х 0, у 0)= 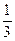 и fу¢ (х 0, у 0)=2. Подставляя найденные значения в формулу (*), получим:
и fу¢ (х 0, у 0)=2. Подставляя найденные значения в формулу (*), получим:  =
=  =
= 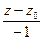 .
.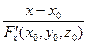 =
=  =
=  .
. ). Здесь F(x, y, z)= x 2+ y 2+ z 2–16, F х¢ (х, у, z)=2 х, F у¢ (х, у, z)=2 у, F z¢ (х, у, z)=2 z, х 0=2, у 0=2, z 0=2
). Здесь F(x, y, z)= x 2+ y 2+ z 2–16, F х¢ (х, у, z)=2 х, F у¢ (х, у, z)=2 у, F z¢ (х, у, z)=2 z, х 0=2, у 0=2, z 0=2  =
=  =
=  .·
.· =
=  .
.  +
+ 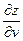 .
.  ,
, 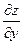 =
=  +
+  .
. , v =
, v =  . Тогда по формулам теоремы 4 получаем:
. Тогда по формулам теоремы 4 получаем:  +3 v 2.
+3 v 2.  ,
,  –3 v 2.
–3 v 2.  . Подставляя выражения для u и v, получим:
. Подставляя выражения для u и v, получим:  .
.  +
+ 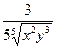 ;
;  –
–  .
. .
.  ,
,  , то есть
, то есть  .cos x =
.cos x = ,
,  .·
.· , то он называется производной функции f (x, y) по направлению l в точке Р0 и обозначается
, то он называется производной функции f (x, y) по направлению l в точке Р0 и обозначается  .
. и
и  =
=  +
+ 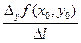 . Заметим, что D l =
. Заметим, что D l = 
 , т.е.
, т.е.  +
+  . Поскольку D l ®0 тогда и только тогда, когда D х ®0 и D у ®0, то
. Поскольку D l ®0 тогда и только тогда, когда D х ®0 и D у ®0, то  +
+ 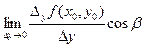 . Так как функция дифференцируема в окрестности точки (х 0, у 0), то это равенство можно переписать так:
. Так как функция дифференцируема в окрестности точки (х 0, у 0), то это равенство можно переписать так: 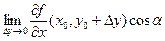 +
+  . Используя непре-
. Используя непре-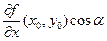 +
+  =
=  =(cosa, cosb) – орт направления l. Тогда из теоремы 5 получаем, что
=(cosa, cosb) – орт направления l. Тогда из теоремы 5 получаем, что  . Тогда частные производные этих функций называются вторыми частными производными функции f (x, y).
. Тогда частные производные этих функций называются вторыми частными производными функции f (x, y). = fx ¢ (
= fx ¢ ( = fу ¢ (
= fу ¢ ( = fx ¢ (
= fx ¢ ( = fу ¢ (
= fу ¢ ( :
: 


