7.1.Несобственный интеграл первого рода
Определение 1. Пусть для любого с > a функция f (x) интегрируема на отрезке [ a; с ]. Если существует 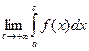 , то он называется несобственным интегралом первого рода функции f (x) и обозначается
, то он называется несобственным интегралом первого рода функции f (x) и обозначается 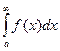 . В этом случае также говорят, что интеграл
. В этом случае также говорят, что интеграл 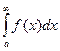 сходится. Если указанный предел не существует, то интеграл расходится.
сходится. Если указанный предел не существует, то интеграл расходится.
Аналогично определяется несобственный интеграл первого рода 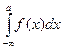 . Если оба интеграла
. Если оба интеграла 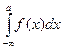 и
и 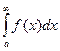 сходятся, то говорят, что сходится интеграл
сходятся, то говорят, что сходится интеграл 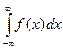 =
= 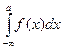 +
+ 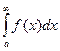 .
.
Примеры. 1) 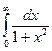 =
= 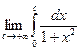 =
= 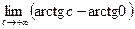 =
= 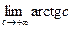 =
=  .
.
Аналогично 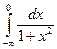 =
=  . А это означает, что
. А это означает, что 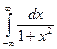 тоже сходится и равен p.
тоже сходится и равен p.
2) 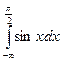 =
= 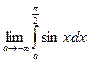 =
= 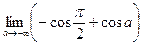 =
= 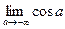 . Этот предел не существует, поэтому интеграл
. Этот предел не существует, поэтому интеграл 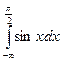 расходится.
расходится.
3) 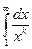 =
= 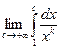 =
= 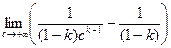 , если k ¹ 1. Этот предел существует и равен
, если k ¹ 1. Этот предел существует и равен 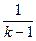 , если k > 1. Если же k < 1, то предел равен бесконечности – интеграл расходится. Интеграл
, если k > 1. Если же k < 1, то предел равен бесконечности – интеграл расходится. Интеграл  тоже расходится:
тоже расходится: 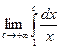 =
= 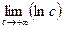 =¥. Итак, интеграл
=¥. Итак, интеграл 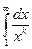 сходится тогда и только тогда, когда k > 1.·
сходится тогда и только тогда, когда k > 1.·
7.2.Несобственный интеграл второго рода
Определение 2. Пусть функция f (x) не ограничена на отрезке [ a; b ], но для любого e> 0 f (x) интегрируема на отрезке [ a; b –e]. Если существует 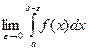 , то он называется несобственным интегралом второго рода функции f (x) и обозначается
, то он называется несобственным интегралом второго рода функции f (x) и обозначается  . В этом случае также говорят, что интеграл
. В этом случае также говорят, что интеграл  сходится. Если указанный предел не существует, то интеграл расходится.
сходится. Если указанный предел не существует, то интеграл расходится.
Аналогично определяется несобственный интеграл второго рода, если функция f (x) не ограничена на отрезке [ a; b ], но интегрируема на отрезке [ a +e; b ] для любого e> 0.
Примеры. 1) 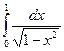 =
= 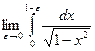 =
= 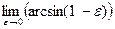 =
=  . Аналогично
. Аналогично 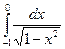 =
= 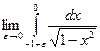 =
= 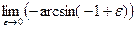 =
=  .
.
Поэтому 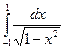 =p.
=p.
2) 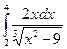 =
= 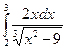 +
+ 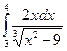 . Каждое слагаемое – несобственный интеграл второго рода. Рассмотрим первый из них:
. Каждое слагаемое – несобственный интеграл второго рода. Рассмотрим первый из них: 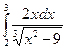 =
= 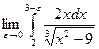 =
= 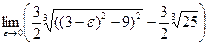 ==
== 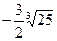 . Аналогично
. Аналогично 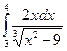 =
= 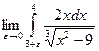 =
=
= 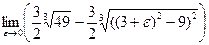 =
= 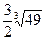 . Значит,
. Значит, 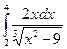 =
=
= 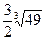
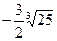 .
.
3) 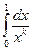 =
= 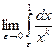 =
= 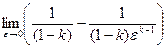 , если k ¹ 1. Этот предел существует и равен
, если k ¹ 1. Этот предел существует и равен 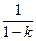 , если k < 1. Если же k > 1, то предел равен бесконечности – интеграл расходится. Интеграл
, если k < 1. Если же k > 1, то предел равен бесконечности – интеграл расходится. Интеграл 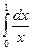 тоже расходится:
тоже расходится: 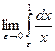 =
= 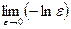 =¥. Итак, интеграл
=¥. Итак, интеграл 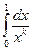 сходится тогда и только тогда, когда k < 1.·
сходится тогда и только тогда, когда k < 1.·
7.3.Признаки сходимости несобственных интегралов
Примем без доказательства следующие признаки сходимости несобственных интегралов – так называемые признаки сравнения.
1. Пусть для любого с > a функции f (x) и g (x) интегрируемы на отрезке [ a; с ], причем 0£ f (x)£ g (x) при х ³ a. Тогда, если интеграл 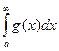 сходится, то и интеграл
сходится, то и интеграл 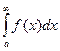 сходится, а если интеграл
сходится, а если интеграл 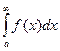 расходится, то и интеграл
расходится, то и интеграл 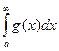 расходится.
расходится.
2. Пусть для любого с > a функции f (x) и g (x) положительны и интегрируемы на отрезке [ a; с ]. Если существует 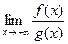 ¹ 0, то интегралы
¹ 0, то интегралы 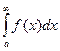 и
и 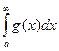 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Следствие 1. Если существует 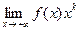 ¹ 0, то интеграл
¹ 0, то интеграл 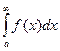 сходится тогда и только тогда, когда k > 1.
сходится тогда и только тогда, когда k > 1.
3. Пусть для любого e> 0 функции f (x) и g (x) интегрируемы на отрезке [ a; b –e], причем 0£ f (x)£ g (x) при a £ х < b. Тогда, если интеграл 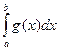 сходится, то и интеграл
сходится, то и интеграл  сходится, а если интеграл
сходится, а если интеграл  расходится, то и интеграл
расходится, то и интеграл 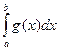 расходится.
расходится.
4. Пусть для любого e> 0 функции f (x) и g (x) положительны и интегрируемы на отрезке [ a; b –e]. Если существует 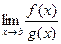 ¹ 0, то интегралы
¹ 0, то интегралы  и
и 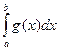 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Следствие 2. Если существует 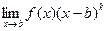 ¹ 0, то интеграл
¹ 0, то интеграл  сходится тогда и только тогда, когда k < 1.
сходится тогда и только тогда, когда k < 1.
Примеры. 1) Рассмотрим 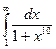 . Поскольку
. Поскольку
0< 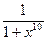 <
< 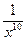 при x ³ 1, а интеграл
при x ³ 1, а интеграл 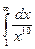 сходится (так как
сходится (так как
показатель 10 больше 1), то по первому признаку сравнения исходный интеграл сходится.
2) Рассмотрим 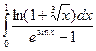 . Поскольку при x ®0 подынтегральная функция эквивалентна дроби
. Поскольку при x ®0 подынтегральная функция эквивалентна дроби 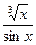 , то есть эквивалентна дроби
, то есть эквивалентна дроби 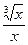 =
= 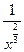 , а интеграл
, а интеграл 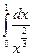 сходится (так как показатель
сходится (так как показатель  меньше 1), то по четвертому признаку сравнения исходный интеграл сходится.
меньше 1), то по четвертому признаку сравнения исходный интеграл сходится.
3) Рассмотрим 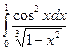 . Если 0£ х < 1, то 0£
. Если 0£ х < 1, то 0£ 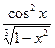 £
£ 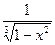 £
£ 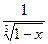 . Интеграл
. Интеграл 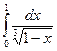 = –
= – 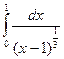 сходится (так как показатель
сходится (так как показатель 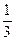 меньше 1). Значит, по третьему признаку сравнения исходный интеграл сходится.
меньше 1). Значит, по третьему признаку сравнения исходный интеграл сходится.
4) Рассмотрим 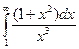 . Поскольку при x ®¥ подынтегральная функция эквивалентна дроби
. Поскольку при x ®¥ подынтегральная функция эквивалентна дроби  , а интеграл
, а интеграл 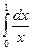 расходится, то по второму признаку сравнения исходный интеграл расходится.·
расходится, то по второму признаку сравнения исходный интеграл расходится.·

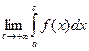 , то он называется несобственным интегралом первого рода функции f (x) и обозначается
, то он называется несобственным интегралом первого рода функции f (x) и обозначается 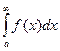 . В этом случае также говорят, что интеграл
. В этом случае также говорят, что интеграл 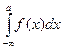 . Если оба интеграла
. Если оба интеграла 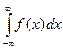 =
= 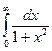 =
= 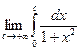 =
= 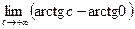 =
= 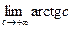 =
=  .
.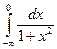 =
= 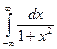 тоже сходится и равен p.
тоже сходится и равен p.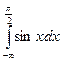 =
= 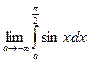 =
= 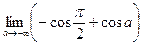 =
= 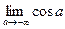 . Этот предел не существует, поэтому интеграл
. Этот предел не существует, поэтому интеграл 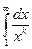 =
= 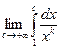 =
= 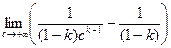 , если k ¹ 1. Этот предел существует и равен
, если k ¹ 1. Этот предел существует и равен 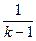 , если k > 1. Если же k < 1, то предел равен бесконечности – интеграл расходится. Интеграл
, если k > 1. Если же k < 1, то предел равен бесконечности – интеграл расходится. Интеграл  тоже расходится:
тоже расходится: 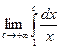 =
= 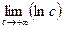 =¥. Итак, интеграл
=¥. Итак, интеграл 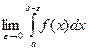 , то он называется несобственным интегралом второго рода функции f (x) и обозначается
, то он называется несобственным интегралом второго рода функции f (x) и обозначается  . В этом случае также говорят, что интеграл
. В этом случае также говорят, что интеграл 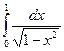 =
= 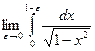 =
= 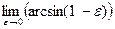 =
= 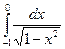 =
= 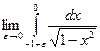 =
= 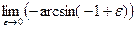 =
= 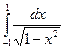 =p.
=p.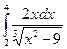 =
= 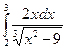 +
+ 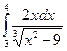 . Каждое слагаемое – несобственный интеграл второго рода. Рассмотрим первый из них:
. Каждое слагаемое – несобственный интеграл второго рода. Рассмотрим первый из них: 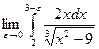 =
= 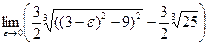 ==
== 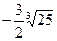 . Аналогично
. Аналогично 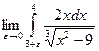 =
=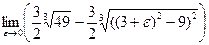 =
= 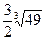 . Значит,
. Значит, 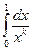 =
= 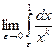 =
= 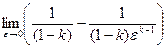 , если k ¹ 1. Этот предел существует и равен
, если k ¹ 1. Этот предел существует и равен 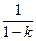 , если k < 1. Если же k > 1, то предел равен бесконечности – интеграл расходится. Интеграл
, если k < 1. Если же k > 1, то предел равен бесконечности – интеграл расходится. Интеграл 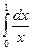 тоже расходится:
тоже расходится: 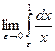 =
= 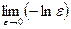 =¥. Итак, интеграл
=¥. Итак, интеграл 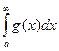 сходится, то и интеграл
сходится, то и интеграл 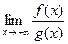 ¹ 0, то интегралы
¹ 0, то интегралы 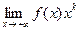 ¹ 0, то интеграл
¹ 0, то интеграл 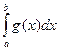 сходится, то и интеграл
сходится, то и интеграл 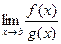 ¹ 0, то интегралы
¹ 0, то интегралы 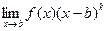 ¹ 0, то интеграл
¹ 0, то интеграл 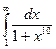 . Поскольку
. Поскольку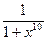 <
< 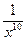 при x ³ 1, а интеграл
при x ³ 1, а интеграл 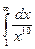 сходится (так как
сходится (так как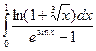 . Поскольку при x ®0 подынтегральная функция эквивалентна дроби
. Поскольку при x ®0 подынтегральная функция эквивалентна дроби 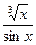 , то есть эквивалентна дроби
, то есть эквивалентна дроби 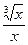 =
= 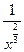 , а интеграл
, а интеграл 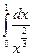 сходится (так как показатель
сходится (так как показатель  меньше 1), то по четвертому признаку сравнения исходный интеграл сходится.
меньше 1), то по четвертому признаку сравнения исходный интеграл сходится.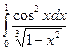 . Если 0£ х < 1, то 0£
. Если 0£ х < 1, то 0£ 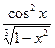 £
£ 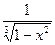 £
£ 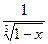 . Интеграл
. Интеграл 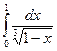 = –
= – 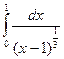 сходится (так как показатель
сходится (так как показатель 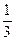 меньше 1). Значит, по третьему признаку сравнения исходный интеграл сходится.
меньше 1). Значит, по третьему признаку сравнения исходный интеграл сходится.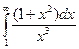 . Поскольку при x ®¥ подынтегральная функция эквивалентна дроби
. Поскольку при x ®¥ подынтегральная функция эквивалентна дроби  , а интеграл
, а интеграл 


