Криволинейные интегралы
3.1.Криволинейный интеграл I рода
Пусть функция f (x, y) определена и непрерывна во всех точках гладкой дуги L=AB, заданной уравнением y =j(x), где a £ x £ b. Рассмотрим разбиение этой дуги точками А0, А1, …, Аn, где А0 = А, Аn = В. Пусть Dsk – длина дуги Ak-1Ak, d = Определение. Если существует предел интегральных сумм I рода при d ®0, не зависящий от разбиения, то этот предел называется криволинейным интегралом I рода функции f (x, y) по дуге L и обозначается Можно доказать, что криволинейный интеграл I рода равен определенному интегралу Если дуга L имеет линейную плотность f (x, y)> 0, то масса этой дуги равна Примем без доказательства свойства аддитивности и линейности криволинейного интеграла I рода. 1о. Если дуга L является объединением дуг L1 и L2, имеющих не более одной общей точки, и существуют 2о. 3о. Важным свойством криволинейного интеграла I рода является его независимость от направления интегрирования: 4о.
3.2.Определение и свойства криволинейного интеграла II рода
Пусть функции P(x, y) и Q(x, y) определены и непрерывны во всех точках гладкой дуги AB, заданной уравнением y =j(x), где a £ x £ b. Рассмотрим разбиение этой дуги точками А0, А1, …, Аn, где А0=А, Аn=В. Обозначим через D x k и D y k проекции дуги Ak-1Ak на ось абсцисс и ось ординат соответственно и выберем на каждой дуге Ak-1Ak точку (xk, hk). Сумма Определение. Если существует предел интегральных сумм II рода при max(D x k)®0 и max(D y k)®0, не зависящий от разбиения, то этот предел называется криволинейным интегралом II рода и обозначается Если плоская гладкая дуга АВ находится в поле действия переменной силы Примем без доказательства свойства криволинейного интеграла II рода. 1о. 2о. Если дуга L является объединением дуг L1 и L2, имеющих не более одной общей точки, и существуют 3о. Если АВ – отрезок, параллельный оси абсцисс, то на этом отрезке y =const, поэтому dy =0, а значит, 4о. Если АВ – отрезок, параллельный оси ординат, то на этом отрезке х =const, поэтому dх =0, а значит, 5о. Важным свойством криволинейного интеграла II рода является его зависимость от направления интегрирования: Замечание. Последнее свойство проще всего понять, используя физический смысл криволинейного интеграла II рода: при движении по дуге в противоположных направлениях одна и та же сила совершает противоположную по знаку работу.
3.3.Вычисление криволинейного интеграла II рода
Пусть функции P(x, y) и Q(x, y) определены и непрерывны во всех точках гладкой дуги AB, заданной уравнением y =j(x), где a £ x £ b. Тогда
Аналогично, если дуга АВ задана уравнением х = y(у), где c £ y £ d, получаем формулу:
Наконец, если дуга АВ задана параметрически: x = x (t), y = y (t), a£ t £ b, – то
Примеры. 1) Найдем а) дуга АВ – часть параболы y = x 2, 0£ x £ 2; б) дуга АВ – часть параболы x = а) б) 2) Найдем 3) Пусть в плоскости x 0 y действует сила а) Работа равна б) Работа равна
= Аналогично на участке СВ равна Замечание. В приведенном примере работа силового поля зависит не только от начального и конечного положения перемещаемой материальной точки, но и от пути перемещения. 3.4.Формула Грина
Рассмотрим область D, ограниченную гладкой замкнутой кривой L. Будем считать положительным такое направление обхода контура L, при котором область D остается слева. Лемма 1. Пусть D – криволинейная трапеция, ограниченная прямыми x = a, x = b (a < b) и гладкими линиями y = g (x), y = h (x), где g (x)≤ h (x) при x Î [ a; b ] (криволинейная трапеция I вида), L – ее граница. Пусть функции P(x, y) и Доказательство.
Аналогично доказывается и следующая лемма. Лемма 2. Пусть D – криволинейная трапеция, ограниченная прямыми y = c, y = d (c < d) и гладкими линиями x = g (y), x = h (y), где g (y)≤ h (y) при y Î [ c; d ] (криволинейная трапеция II вида), L – ее граница. Пусть функции Q(x, y) и Следствие. Формулы из лемм 1 и 2 верны, если область D – объединение конечного числа криволинейных трапеций I и II вида, не имеющих общих внутренних точек. Отсюда вытекает следующая теорема. Теорема 1. Пусть область D – объединение конечного числа криволинейных трапеций I и II вида, не имеющих общих внутренних точек, L – ее граница; функции P(x, y), Q(x, y),
Пример. Вычислим с помощью формулы Грина =
3.5.Условие независимости криволинейного интеграла II рода от пути интегрирования Будем называть область D односвязной, если любая замкнутая линия, содержащаяся в D, ограничивает область, полностью лежащую в D. Теорема 2. Пусть функции P(x, y), Q(x, y), Доказательство. Þ Пусть, например, Ü Если Теорема 3. Пусть функции P(x, y), Q(x, y), Доказательство. Þ Пусть данные точки соединены двумя гладкими кривыми L1 и L2. Тогда они образуют гладкий контур L, целиком лежащий в Е. Ü Пусть данные точки соединены двумя гладкими кривыми L1 и L2. Тогда они образуют гладкий контур L, целиком лежащий в Е. Так как в любой внутренней точке области Пример. Рассмотрим 3.6.Восстановление функции по полному дифференциалу
Выражение P(x, y) dx +Q(x, y) dy будем называть полным дифференциалом, если существует функция z (x, y) (называемая первообразной полного дифференциала) такая, что dz =P(x, y) dx +Q(x, y) dy. Теорема 4. Пусть функции P(x, y), Q(x, y), Доказательство. Þ Пусть dz =P dx +Q dy. Тогда в любой внутренней точке области Ü Фиксируем А(x o, y o)Î E. Пусть М(x, y)Î E – произвольная. Тогда 1о. v (x, y) = 2о. v (x +D x, y) = 3о. D xv = 4о. 5o. Аналогично
Пример. Докажем, что выражение (2 x cos y – y 2sin x) dx + (2 y cos x – x 2sin y) dy является полным дифференциалом. Здесь P(x, y)=2 x cos y – y 2sin x, z (x, y)=
|

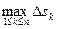 – диаметр разбиения. Выберем на каждой дуге Ak-1Ak точку (xk, hk). Сумма
– диаметр разбиения. Выберем на каждой дуге Ak-1Ak точку (xk, hk). Сумма  Dsk называется интегральной суммой I рода.
Dsk называется интегральной суммой I рода.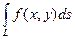 .
.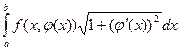 . Если же кривая L задана параметрически уравнениями x = x (t), y = y (t), a£ t £ b, то криволинейный интеграл I рода равен
. Если же кривая L задана параметрически уравнениями x = x (t), y = y (t), a£ t £ b, то криволинейный интеграл I рода равен 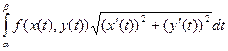 .
.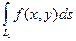 и
и 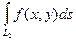 , то существует и
, то существует и  =
= 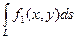 +
+ 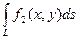 .
. = l
= l 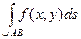 =
=  .
.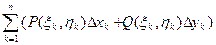 называется интегральной суммой II рода.
называется интегральной суммой II рода. .
.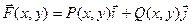 , то работа этой силы при перемещении материальной точки по дуге АВ равна
, то работа этой силы при перемещении материальной точки по дуге АВ равна 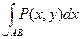 +
+ 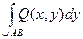 .
.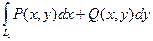 и
и  , то существует и
, то существует и 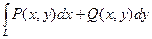 , равный их сумме (свойство аддитивности).
, равный их сумме (свойство аддитивности).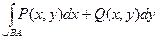 .
.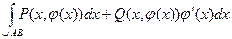 (мы заменили y на
(мы заменили y на  ), и значит,
), и значит,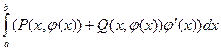 .
.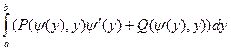 .
.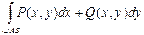 =
= 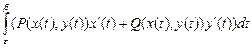 .
. в двух случаях:
в двух случаях: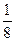 y 2, 0£ y £ 4.
y 2, 0£ y £ 4.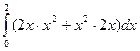 =
= 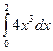 =
= 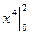 =16.
=16.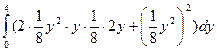 = =
= =  =
= 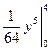 =16.
=16.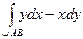 , где дуга АВ – единичная окружность с центром в начале координат. Для этого зададим окружность параметрически: x =cos t, y =sin t, 0£ t £ 2p. Тогда
, где дуга АВ – единичная окружность с центром в начале координат. Для этого зададим окружность параметрически: x =cos t, y =sin t, 0£ t £ 2p. Тогда 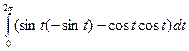 =
=  –2p.
–2p.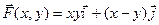 . Найдем работу этой силы при перемещении из точки А(1; 0) в точку В(2; 3), если путь представляет собой: а) отрезок АВ; б) ломаную АСВ, где С(2; 0).
. Найдем работу этой силы при перемещении из точки А(1; 0) в точку В(2; 3), если путь представляет собой: а) отрезок АВ; б) ломаную АСВ, где С(2; 0).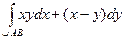 . Найдем уравнение отрезка АВ:
. Найдем уравнение отрезка АВ: 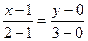 , 1£ x £ 2, то есть у =3 х –3, 1£ x £ 2. Значит,
, 1£ x £ 2, то есть у =3 х –3, 1£ x £ 2. Значит, 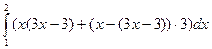 =
= 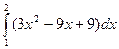 =
= 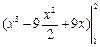 =(8–18+18)–(1–4, 5+9) =2, 5.
=(8–18+18)–(1–4, 5+9) =2, 5.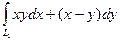 +
+ 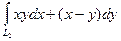 , где L1 – отрезок АС, L2 – отрезок СВ. Уравнение отрезка АС: у =0, 1£ х £ 2; уравнение отрезка СВ: х =2, 0£ у £ 3. Так как отрезок АС параллелен оси абсцисс, то
, где L1 – отрезок АС, L2 – отрезок СВ. Уравнение отрезка АС: у =0, 1£ х £ 2; уравнение отрезка СВ: х =2, 0£ у £ 3. Так как отрезок АС параллелен оси абсцисс, то  =
=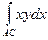 . Значит, работа на отрезке АС равна
. Значит, работа на отрезке АС равна 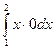 =0.
=0.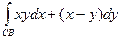 =
= 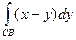 , то есть работа
, то есть работа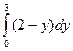 =
=  = 1, 5.·
= 1, 5.·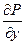 (x, y) непрерывны в области D. Тогда
(x, y) непрерывны в области D. Тогда  = –
= – 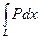 .
.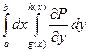 =
=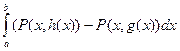 =
= 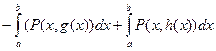 =
= 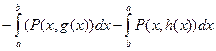 . Так как интегралы
. Так как интегралы 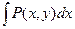 по вертикальным отрезкам контура равны нулю, то полученная разность противоположна интегралу по всему контуру, то есть равна –
по вертикальным отрезкам контура равны нулю, то полученная разность противоположна интегралу по всему контуру, то есть равна –  (x, y) непрерывны в области D. Тогда
(x, y) непрерывны в области D. Тогда  =
= 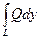 .
.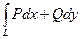 =
= 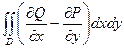 .
.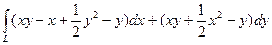 , где L – граница области, ограниченной линиями y = x 2–3 x –2, y = x +3. Здесь P(x, y)=
, где L – граница области, ограниченной линиями y = x 2–3 x –2, y = x +3. Здесь P(x, y)=  ,
, 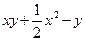 ,
, 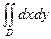 , где D – область, ограниченная линиями y = x 2–3 x –2, y = x +3.
, где D – область, ограниченная линиями y = x 2–3 x –2, y = x +3. 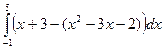 =
= 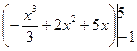 =36.·
=36.·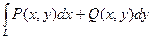 =0, так как интегралы по L1 и по L2 берутся с противоположными знаками. Значит, по теореме 2 в любой внутренней точке области
=0, так как интегралы по L1 и по L2 берутся с противоположными знаками. Значит, по теореме 2 в любой внутренней точке области 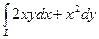 , где кривая L задана формулами x = t cos2 t, y = t (cos t +1), 0≤ t ≤ p. Здесь P(x, y)=2 ху,
, где кривая L задана формулами x = t cos2 t, y = t (cos t +1), 0≤ t ≤ p. Здесь P(x, y)=2 ху, 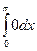 =0.·
=0.· ,
, 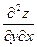 . Так как P, Q,
. Так как P, Q,  , где L1 соединяет точки М(x, y) и N(x +D x, y).
, где L1 соединяет точки М(x, y) и N(x +D x, y).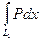 =
= 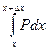 =P(c, y)D x (по теореме о среднем).
=P(c, y)D x (по теореме о среднем).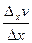 = P(с, y).
= P(с, y).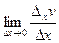 = P(x, y) (так как функция P(x, y) непрерывна), значит,
= P(x, y) (так как функция P(x, y) непрерывна), значит, 
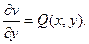 Значит, P dx +Q dy = dv – полный дифференциал. Теорема доказана полностью.
Значит, P dx +Q dy = dv – полный дифференциал. Теорема доказана полностью.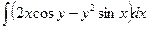 = x 2cos y + y 2cos x +C(y). Тогда
= x 2cos y + y 2cos x +C(y). Тогда 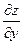 = – х 2sin y +2 y cos x +C¢ (y). Но
= – х 2sin y +2 y cos x +C¢ (y). Но 


