Вычисление определенного интеграла
5.1.Существование первообразной для непрерывной функции Пусть функция f (x) непрерывна на отрезке [ a; b ]. Тогда она интегрируема на любом отрезке [ a; х ], если х Î [ a; b ]. Поэтому на отрезке [ a; b ] можно определить функцию Ф(x)= Теорема 1. Если функция f (x) непрерывна на отрезке [ a; b ], то функция Ф(x)= Доказательство. Рассмотрим приращение функции Ф(x): DФ= Следствие. Функция, непрерывная на отрезке, имеет на этом отрезке первообразную. 5.2.Формула Ньютона-Лейбница Теорема 2. Если функция f (x) непрерывна на отрезке [ a; b ] и F(x) – ее первообразная, то Доказательство. Поскольку F(x) и Ф(x)= Разность F(b)–F(a) обозначают F(х) Пример. Так как 5.3.Свойства определенного интеграла
1. Если функции f (x) и g (x) интегрируемы на отрезке [ a; b ], a и b – числа, то Действительно, если F(x) и G(x) – первообразные соответственно функций f (x) и g (x), то по свойству линейности неопределенного интеграла aF(x)+bG(x) – первообразная функции a f (x)+b g (x). По формуле Ньютона-Лейбница 2. Если функция f (x) непрерывна и положительна на отрезке [ a; b ], то Действительно, по теореме о среднем значении 3. Если функции f (x) и g (x) непрерывны на отрезке [ a; b ], причем f (x)³ g (x), то Действительно, по свойству линейности – Пример. =(
5.4.Замена переменной в определенном интеграле
Правило замены переменной в неопределенном интеграле и формула Ньютона-Лейбница позволяют обосновать следующее утверждение. Пусть функция f (x) интегрируема на отрезке [ a; b ], а x =j(t) – непрерывная на отрезке [a; b] и дифференцируемая на интервале (a; b) функция, принимающая значения на отрезке [ a; b ], причем j(a)= a; j(b)= b. Тогда Примеры. 1) = = 2) =
5.5.Интегрирование по частям в определенном интеграле Правило интегрирования по частям в неопределенном интеграле и формула Ньютона-Лейбница позволяют обосновать следующее утверждение. Если функции u (x) и v (x) дифференцируемы на отрезке [ a; b ], то Пример. – =0, 75 e 4–0, 25 e 2.·
|

 .
.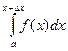 –
–  . А по теореме о среднем значении существует такое с Î [ х; х +D х ], что
. А по теореме о среднем значении существует такое с Î [ х; х +D х ], что 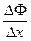 = f (с), с Î [ х; х +D х ]. Тогда в силу непрерывности функции f (x)
= f (с), с Î [ х; х +D х ]. Тогда в силу непрерывности функции f (x)  = f (x), ч.т.д.
= f (x), ч.т.д. =F(b)–F(a).
=F(b)–F(a). +С, F(b)=
+С, F(b)=  .
. =
= 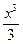 +С, то
+С, то 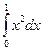 =
=  =
= 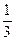 .·
.· =
=  +
+  . Это свойство называют свойством линейности.
. Это свойство называют свойством линейности.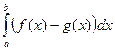 , а по свойству 2 этот интеграл неотрицателен, ч.т.д.
, а по свойству 2 этот интеграл неотрицателен, ч.т.д.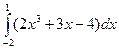 =(2.
=(2.  +3.
+3.  –4 х)
–4 х)  =
=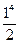 +3.
+3. 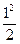 –4.1)–(
–4.1)–(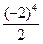 +3.
+3. 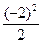 –4.(–2))= –2–22= –24.·
–4.(–2))= –2–22= –24.·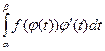 .
. =
= 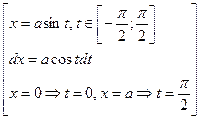
 =
=  =
=  . Последнее равенство верно потому, что на данном отрезке cos t ³ 0, то есть ï cos t ï =cos t.
. Последнее равенство верно потому, что на данном отрезке cos t ³ 0, то есть ï cos t ï =cos t.  =
=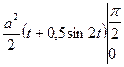 =
=  . Заметим, что
. Заметим, что 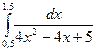 =
=  =
=  =
=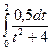 =0, 25arctg
=0, 25arctg 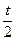
 =0, 25(arctg1–arctg0)=
=0, 25(arctg1–arctg0)= 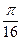 .·
.·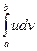 = uv
= uv  .
.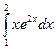 =
=  =0, 5 xe 2 x
=0, 5 xe 2 x  –
–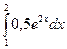 =0, 5(2 e 4– e 2)–0, 25 e 2 x
=0, 5(2 e 4– e 2)–0, 25 e 2 x 


