Методы интегрирования
2.1. Замена переменной Теорема 1. Пусть F(x) – первообразная функции f (x) на отрезке [ a; b ], а x =j(t) – непрерывная на отрезке [a; b] и дифференцируемая на интервале (a; b) функция, принимающая значения на отрезке [ a; b ]. Тогда функция F(j(t)) является первообразной функции f (j(t))j¢ (t) на отрезке [a; b]. Доказательство. По теореме о производной сложной функции (F(j(t)))¢ = F¢ (j(t))j¢ (t). Поскольку F¢ (х)= f (x), получаем (F(j(t)))¢ = f (j(t))j¢ (t), ч.т.д. Другими словами, если ò f (x) dx =F(x)+C, то ò f (j(х))j¢ (х) dx =F(j(х))+C. Примеры. 1) 2)
Из теоремы 1 вытекает так называемая теорема о линейной замене. Теорема 2. Пусть F(x) – первообразная функции f (x) и а ¹ 0. Тогда функция Примеры. 1) 2) 2.2. Интегрирование по частям Теорема 3. Если функции u (x) и v (x) дифференцируемы на отрезке [ a; b ], то ò u (х) dv (х) = u (x) v (x)– ò v (х) du (х). Эта формула называется формулой интегрирования по частям. Доказательство. По формуле дифференциала произведения получаем: d (uv)= vdu + udv, откуда ò d (uv)= ò vdu +ò udv, то есть uv = ò vdu +ò udv, ò udv = uv –ò vdu, ч.т.д. Примеры. 1)Рассмотрим ò x sin xdx. Пусть x = u, тогда sin xdx = dv, значит, v =–cos x, du = dx. По формуле интегрирования по частям получаем: ò x sin xdx = x (–cos x)– ò (–cos x) dx. Значит, ò x sin xdx = – x cos x + ò cos xdx = – x cos x +sin x +C. 2)Рассмотрим ò ln xdx. Пусть ln x = u, тогда dx = dv, значит, v = x, du =
|

 =
=  . Поскольку
. Поскольку  = ех +C, получаем:
= ех +C, получаем:  =
= 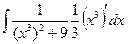 =
= 
 . Поскольку
. Поскольку 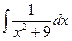 =
=  , получаем:
, получаем:  arctg
arctg 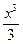 +C.·
+C.· F(ax + b) является первообразной функции f (ax + b).
F(ax + b) является первообразной функции f (ax + b). =
=  lnï 5 x –3ï, так как
lnï 5 x –3ï, так как  = lnï x ï +C.
= lnï x ï +C. =lnï x – а ï +С.·
=lnï x – а ï +С.· dx. По формуле интегрирования по частям: ò ln xdx =ln x . x –ò x
dx. По формуле интегрирования по частям: ò ln xdx =ln x . x –ò x 


