Геометрические и механические приложения
определенного интеграла 6.1.Площадь плоской фигуры Пусть функции f (x) и g (x) непрерывны на отрезке [ a; b ], причем f (x)³ g (x). Тогда площадь фигуры, ограниченной линиями x = a, x = b, y = f (x), y = g (x), можно найти по формуле: S= Примеры. 1) Найдем площадь фигуры, ограниченной линиями x =1, x =2, y =5– x, y = x. На отрезке [1; 2] имеем 5– x > x. Значит, S= 2) Найдем площадь фигуры, ограниченной линиями y = x –2 и y = x 2–4 х +2. Эти линии пересекаются при x =1 и x =4. На отрезке [1; 4] имеем x –2³ x 2–4 х +2. Значит, S= = 3) Найдем площадь фигуры, ограниченной линиями y =ï x –2ï и y = S= = – Если фигура ограничена линией, заданной в полярных координатах: r=r(j), – и лучами j=a и j=b (a< b), то ее площадь можно найти по формуле: S= Пример. Найдем площадь фигуры, ограниченной линией r2=2cos2j и лучами j=0 и j= =0, 5sin2j 6.2.Длина гладкой дуги Пусть дуга представляет собой часть графика функции у = f (x), имеющей на отрезке [ a; b ] непрерывную производную. Такая дуга называется гладкой. Ее длину можно найти по формуле: L= Пример. Найдем длину части цепной линии y =ch x при 0£ x £ 1.L= Пусть дуга задана параметрически: х = х (t), у = y (t), где tÎ [ a; b ], – причем функции х (t) и y (t) имеют на отрезке [ a; b ] непрерывные производные. Тогда длину дуги можно найти по формуле: L= Пример. Найдем длину части астроиды x =cos3 t, y =sin3 t при 0£ t £ = = Пусть дуга задана в полярных координатах: r=r(j), jÎ [a; b], – причем функция r(j) имеет на отрезке [a; b] непрерывную производную. Тогда длину дуги можно найти по формуле: L= Пример. Найдем длину части окружности r=2cosj при 0£ j£ 6.3.Объем тела Рассмотрим тело, заключенное между плоскостями х = а и х = b (a < b). Пусть S(x) – площадь его сечения плоскостью, проходящей через точку х оси абсцисс перпендикулярно этой оси, причем функция S(x) непрерывна на отрезке [ а; b ]. Тогда объем тела можно найти по формуле: V= В частности, для тела, полученного вращением криволинейной трапеции, ограниченной линиями x = a, x = b, y = f (x), y =0 (a < b, f (x)³ 0), около оси абсцисс, каждое сечение – круг радиуса f (x). Значит, площадь сечения равна p(f (x))2 и формула объема тела вращения: V=p Примеры. 1) Рассмотрим пирамиду, высота которой представляет собой отрезок оси абсцисс от 0 до H, а основание лежит в плоскости y O z и имеет площадь S. Тогда площадь S(x) сечения, проходящего через точку х оси абсцисс перпендикулярно этой оси, равна S = 2) Рассмотрим шар с центром в начале координат и радиусом R. Он представляет собой тело, полученное вращением полукруга, ограниченного линиями x =–R, x =R, y =0, y = 3) Рассмотрим конус, высота которого представляет собой отрезок оси абсцисс от 0 до H, а основание лежит в плоскости y O z и имеет радиус R. Он представляет собой тело, полученное вращением треугольника, ограниченного линиями x =0, x =H, y =0, y = =p 6.4.Центр масс и моменты инерции 1. Координаты центра масс гладкой однородной дуги, заданной уравнением y = f (x), a £ x £ b, можно найти по формулам: х о= Координаты центра масс однородной пластины, ограниченной линиями x = a, x = b, y = f (x), y =0 (a < b, f (x)³ 0), можно найти по формулам: х о= Примеры. 1) Найдем координаты центра масс однородной дуги цепной линии: y =ch x, –1£ x £ 1. х о= = 2) Найдем координаты центра масс однородной пластины, представляющей собой часть эллипса x =4cos t, y =3sin t, лежащую в первой четверти. х о= у о= 2. Величину моментов инерции относительно осей О х и О у для гладкой однородной дуги, заданной уравнением y = f (x), a £ x £ b, можно найти соответственно по формулам: I х = Величину моментов инерции относительно осей О х и О у для однородной пластины, ограниченной линиями x = a, x = b, y = f (x), y =0 (a < b, f (x)³ 0), можно найти соответственно по формулам: I х = Примеры. 1) Найдем момент инерции I х для однородной полуокружности: y = I х = 2) Найдем момент инерции I у для однородной пластины, ограниченной эллипсом x =4cos t, y =3sin t. I у = =
|

 .
. =
=  =(5 х – х 2)
=(5 х – х 2)  =6–4=2.
=6–4=2. =
= 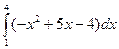 =
= =
=  –
–  =4, 5.
=4, 5. . Эти линии пересекаются при x =1 и x =4. На отрезке [1; 4] имеем
. Эти линии пересекаются при x =1 и x =4. На отрезке [1; 4] имеем  =
= 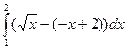 +
+  =
= +
+  =
=  –
– +
+  –
–  =
= 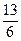 .·
.· .
. : S=
: S=  =
= =0, 5.·
=0, 5.· .
. =
=  =sh x
=sh x  =sh1 =0, 5(e – e –1).·
=sh1 =0, 5(e – e –1).· .
. . L=
. L=  =
= =
=  =
= =
=  =
=  =1, 5.·
=1, 5.· .
. . L=
. L=  =
=  =
=  .·
.· .
. .
. . Находим объем пирамиды: V=
. Находим объем пирамиды: V=  =
= =
= 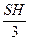 .
. , около оси абсцисс. По формуле объема тела вращения V=p
, около оси абсцисс. По формуле объема тела вращения V=p 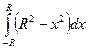 =p
=p  =
= 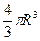 .
. (H– x), около оси абсцисс. По формуле объема тела вращения V=p
(H– x), около оси абсцисс. По формуле объема тела вращения V=p  =
= =
=  .·
.· , у о=
, у о=  .
. , у о=
, у о=  .
. =
=  = x sh x
= x sh x  –
–  =sh1–sh1–ch1 +ch1=0. у о=
=sh1–sh1–ch1 +ch1=0. у о= 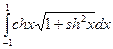 =
= 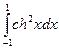 =
=  =
= =1+0, 5sh2.
=1+0, 5sh2.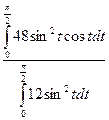 =
=  =
=  .
. =
=  =
=  .·
.· , I у =
, I у =  .
. , I у =
, I у =  .
. , –1£ x £ 1.
, –1£ x £ 1. =
=  =
=  =
=  =
= 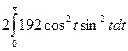 =
=  =
= =48p.·
=48p.·


