Тройные интегралы
Пусть VÍ R 3 – замкнутая область, ограниченная непрерывной поверхностью. Пусть f (x, y, z) – функция, заданная и ограниченная на V. Пусть V = V1È V2È … È Vn, где V1, V2, … Vn – области, не имеющие общих внутренних точек. Обозначим через v k объем области Vk, а через d k – ее диаметр. Пусть d = Определение. Если существует предел интегральных сумм при d ®0, не зависящий от разбиения, то функция f (x, y, z) называется интегрируемой в области V, а предел интегральных сумм называется тройным интегралом функции f (x, y, z) по области V и обозначается 1о. Если функция f (x, y, z) непрерывна в области V, то она интегрируема в этой области. 2о. Пусть область V заполняет неоднородное тело, точечная плотность которого в точке (x, y, z) равна r(x, y, z). Тогда масса этого тела равна Все свойства тройного интеграла повторяют свойства двойного: аддитивность, линейность, неравенства, теорема о среднем. При этом Пусть область V ограничена гладкими поверхностями z =j(x, y) и z =y(x, y), где (x, y)Î D (проекция области V на плоскость x 0 y), причем j(x, y)£ y(x, y) при (x, y)Î D. Тогда Пример. 1) Вычислим 2) Вычислим
|

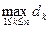 – диаметр разбиения V1, V2, … Vn. В каждой области Vk выберем точку (
– диаметр разбиения V1, V2, … Vn. В каждой области Vk выберем точку ( , zk) и составим интегральную сумму, соответствующую данному разбиению: S =
, zk) и составим интегральную сумму, соответствующую данному разбиению: S = 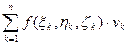 .
. .
.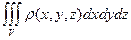 (физический смысл тройного интеграла).
(физический смысл тройного интеграла).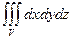 равен объему области V (геометрический смысл тройного интеграла).
равен объему области V (геометрический смысл тройного интеграла). , то есть вычисление тройного интеграла сводится к вычислению двойного и одинарного.
, то есть вычисление тройного интеграла сводится к вычислению двойного и одинарного.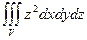 , где область V ограничена параболоидом z = x 2+ y 2 и плоскостью z =1. Проекция D этой области на плоскость х 0 у – круг x 2+ y 2£ 1. Поэтому
, где область V ограничена параболоидом z = x 2+ y 2 и плоскостью z =1. Проекция D этой области на плоскость х 0 у – круг x 2+ y 2£ 1. Поэтому 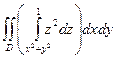 =
= 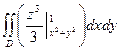 = =
= =  . Перейдем к полярным координатам:
. Перейдем к полярным координатам: 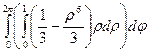 = =
= = 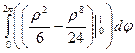 =
= 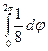 =
= 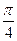 .
.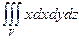 , где V – тетраэдр, ограниченный координатными плоскостями и плоскостью 2 х +2 у + z –6 = 0. Проекция D этого тетраэдра на плоскость х 0 у – треугольник ОАВ, где О – начало координат; уравнение прямой АВ: х + у –3=0, А(3; 0; 0), В(0; 3; 0). Поэтому
, где V – тетраэдр, ограниченный координатными плоскостями и плоскостью 2 х +2 у + z –6 = 0. Проекция D этого тетраэдра на плоскость х 0 у – треугольник ОАВ, где О – начало координат; уравнение прямой АВ: х + у –3=0, А(3; 0; 0), В(0; 3; 0). Поэтому  =
= 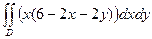 = =
= = 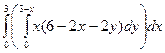 =
=  = =
= = 
 =
=  =
= 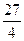 .·
.·


