Двойные интегралы
1.1.Определение двойного интеграла Пусть DÍ R 2 – замкнутая область, ограниченная непрерывной кривой. Пусть f (x, y) – функция, заданная и ограниченная на D. Пусть D = D1È D2È … È Dn, где D1, D2, … Dn – области, не имеющие общих внутренних точек. Обозначим через Sk площадь области Dk, а через d k – ее диаметр (наибольшее расстояние между точками данного множества). Набор D1, D2, … Dn назовем разбиением области D. Пусть d = S = Определение. Если существует предел интегральных сумм при d ®0, не зависящий от разбиения, то функция f (x, y) называется интегрируемой в области D, а предел интегральных сумм называется двойным интегралом функции f (x, y) по области D и обозначается Примем без доказательства следующие утверждения. 1о. Если функция f (x, y) непрерывна в области D, то она интегрируема в этой области. 2о. Пусть в плоскости R 2 область D занята неоднородной пластиной, точечная плотность которой в точке (x, y) равна r(x, y). Тогда масса этой пластины равна 3о. Пусть DÍ R 2 и DÍ D(f), где f (x, y) – неотрицательная функция. Тогда объем цилиндрического бруса, ограниченного снизу областью D, а сверху – поверхностью z = f (x, y), равен 1.2.Свойства двойного интеграла 1о. Доказательство. Составим интегральную сумму для функции f (x, y)=1. Тогда эта сумма равна сумме площадей областей Dk, то есть равна площади области D. Значит, все интегральные суммы одинаковы, поэтому их предел тоже равен площади области D, ч.т.д. 2о. Доказательство. Каждая интегральная сумма для функции l f (x, y) получается из интегральной суммы для функции f (x, y) умножением на l. Значит, и предел интегральных сумм для первой функции равен пределу интегральных сумм для второй функции, умноженному на l, то есть 3о. Доказательство. Каждая интегральная сумма для функции f 1(x, y)+ f 2(x, y) является суммой интегральных сумм для функций f 1(x, y) и f 2(x, y). Значит, и предел интегральных сумм для первой функции равен сумме пределов интегральных сумм для функций f 1(x, y) и f 2(x, y), то есть Свойства 2о и 3о – это свойства линейности двойного интеграла. 4о. Если функция f (x, y) интегрируема и неотрицательна в области D, то ее интеграл по этой области – неотрицательное число. Доказательство. В любой интегральной сумме каждое слагаемое неотрицательно (неотрицательное значение функции умножается на положительное число – площадь области Dk). Значит, и предел интегральных сумм – число неотрицательное, ч.т.д. 5о. Если функции f (x, y) и g (x, y) интегрируемы в области D, причем f (x, y)³ g (x, y), то (Следствие предыдущего утверждения). 6о. Аддитивность двойного интеграла. Если область D разбита на две области D1 и D2, не имеющие общих внутренних точек, и функция f (x, y) интегрируема в каждой из этих двух областей, то эта функция интегрируема и в области D, причем (Без доказательства). 7о. Теорема о среднем. Если функция f (x, y) непрерывна в области D, то существует точка (x, h)Î D такая, что (Без доказательства). 1.3.Вычисление двойного интеграла Пусть D – криволинейная трапеция, ограниченная линиями x = a, x = b, y = g (x), y = h (x), где g (x)£ h (x) при x Î [ a; b ] (так называемая криволинейная трапеция I типа). Пусть f (x, y) – неотрицательная непрерывная на D функция. Рассмотрим цилиндрический брус с основанием D, ограниченный сверху поверхностью z = f (x, y). Пересечем этот брус плоскостью x = t и обозначим через S(t) площадь сечения. Тогда объем бруса равен S(t)=
Эта формула справедлива для любой функции, непрерывной на криволинейной трапеции I типа. Замечания. 1) Для криволинейной трапеции II типа (ограниченной линиями y = c, y = d, x = g (y), x = h (y), где g (y)£ h (y) при y Î [ c; d ]) формула (1) видоизменяется так:
2) При вычислении «внутреннего» интеграла та переменная, по которой интегрирование не ведется, считается константой. Примеры. 1) Вычислим двойной интеграл = = Аналогично, поскольку x £ 2 при x Î [1; 2], то для второй криволинейной трапеции получаем:
Итак, Заметим, что область D можно рассматривать как криволинейную трапецию второго типа, ограниченную линиями y =1, y =2, x = = 2) Найдем объем тела, ограниченного координатными плоскостями, круговым цилиндром x 2+ y 2=R2 и гиперболическим параболоидом z = xy, где x ³ 0, y ³ 0, z ³ 0. Это тело представляет собой цилиндрический брус, основанием которого является область D – четверть круга в плоскости x 0 y (x 2+ y 2=R2, где x ³ 0, y ³ 0), а сверху его ограничивает поверхность z = xy. Значит, объем этого цилиндрического бруса равен 1.4.Вычисление двойного интеграла в полярных координатах В некоторых случаях бывает удобно пользоваться следующей формулой, которую мы примем без доказательства:
Если область D ограничена лучами j=a, j=b (a< b) и линиями r=r1(j) и r=r2(j), где r1(j)£ r2(j) при a£ j£ b, то это равенство переписывается в виде:
Пример. Вычислим
= =
|

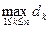 – диаметр разбиения. В каждой области Dk выберем точку (
– диаметр разбиения. В каждой области Dk выберем точку ( ) и составим интегральную сумму, соответствующую данному разбиению:
) и составим интегральную сумму, соответствующую данному разбиению: .
. .
. (физический смысл двойного интеграла).
(физический смысл двойного интеграла).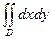 равен площади области D.
равен площади области D. = l
= l  =
=  +
+  .
. .
. +
+  .
. . Спроецируем сечение на плоскость y O z. Получим криволинейную трапецию, ограниченную линиями: y = g (t), y = h (t), z =0, z = f (t, y). Значит,
. Спроецируем сечение на плоскость y O z. Получим криволинейную трапецию, ограниченную линиями: y = g (t), y = h (t), z =0, z = f (t, y). Значит, . Итак, объем бруса равен
. Итак, объем бруса равен  , или
, или  . Но объем бруса равен двойному интегралу функции f (x, y) по области D. Итак, для криволинейной трапеции I типа и для неотрицательной функции f (x, y) мы получили формулу:
. Но объем бруса равен двойному интегралу функции f (x, y) по области D. Итак, для криволинейной трапеции I типа и для неотрицательной функции f (x, y) мы получили формулу: . (2)
. (2)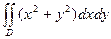 , где область D ограничена линиями y =2, y = x, xy =1. Изобразим область D на координатной плоскости. Линии y = x и xy =1 пересекаются в точке (1; 1), линии y = x и y =2 – в точке (2; 2), а линии y =2 и xy =1 – в точке (0, 5; 2). Поэтому область D – объединение двух криволинейных трапеций I типа: D1 (ограничена линиями x =0, 5, x =1, y =
, где область D ограничена линиями y =2, y = x, xy =1. Изобразим область D на координатной плоскости. Линии y = x и xy =1 пересекаются в точке (1; 1), линии y = x и y =2 – в точке (2; 2), а линии y =2 и xy =1 – в точке (0, 5; 2). Поэтому область D – объединение двух криволинейных трапеций I типа: D1 (ограничена линиями x =0, 5, x =1, y =  и y =2) и D2 (ограничена линиями x =1, x =2, y = x и y =2). Значит,
и y =2) и D2 (ограничена линиями x =1, x =2, y = x и y =2). Значит,  +
+  . Поскольку
. Поскольку 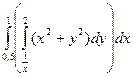 =
=  =
=  =
= 
 =
=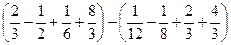 =
=  .
. =
=  =
=  ==
==  =
=  = =
= =  =
=  .
. .
. и x = y. Поскольку
и x = y. Поскольку  =
=  =
=  =
= 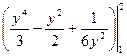 =
= =
=  . Область D представляет собой криволинейную трапецию I типа, ограниченную линиями x =0, x =R, y =0, y =
. Область D представляет собой криволинейную трапецию I типа, ограниченную линиями x =0, x =R, y =0, y =  . Значит,
. Значит,  =
=  =
=  =
=  =
= 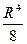 .·
.·
 .
.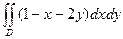 , где D – сектор круга x 2+ y 2£ 4, лежащий в III четверти между прямыми y = x и у = х
, где D – сектор круга x 2+ y 2£ 4, лежащий в III четверти между прямыми y = x и у = х  . Для этого заметим, что в третьей четверти на луче прямой y = x угол j= –p+arctg1= –
. Для этого заметим, что в третьей четверти на луче прямой y = x угол j= –p+arctg1= –  , а на луче прямой y = x
, а на луче прямой y = x  . Область D ограничена этими лучами и линиями r=0 и r=2. Значит,
. Область D ограничена этими лучами и линиями r=0 и r=2. Значит, =
= =
= =(2j –
=(2j –  sinj+
sinj+  cosj)
cosj)  = =
= =  .·
.·


