ТЕНИ В ПЕРСПЕКТИВЕ

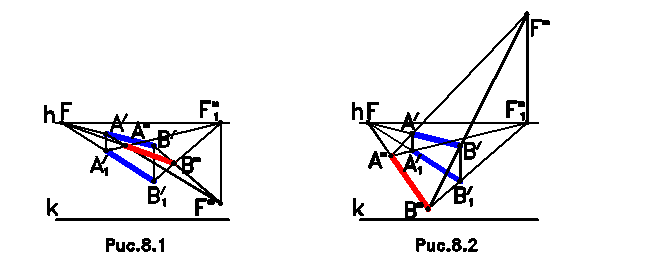
Изображение теней придает перспективе дополнительную выразительность и объемность. Направление световых лучей в отличие от комплексного чертежа может быть произвольным. При этом возможны три случая расположения параллельных световых лучей, идущих от солнца: лучи направлены от наблюдателя к объекту, лучи направлены от объекта к наблюдателю, лучи параллельны картинной плоскости (фронтальное положение лучей). При этом угол наклона лучей может быть произвольным в каждом из этих случаев. Для построения теней в перспективе необходимо знать перспективную проекцию луча, а также его вторичную перспективную проекцию. На рис.8.1 – 8.3 показано построение теней на предметную плоскость от горизонтального отрезка в каждом из вышеперечисленных случаев. Параллельные лучи будут иметь общую точку схода. Точка схода вторичных проекций лучей F₁^т находится на линии горизонта. Точка схода перспективной проекции лучей F^т в первом случае находится ниже линии горизонта (рис.8.1), во втором случае (рис.8.2) – выше линии горизонта, в третьем случае (рис.8.3) – точка схода отсутствует. Перспективная проекция тени A^т от точки A находится в пересечении вторичной проекции светового луча, направленного из вторичной проекции точки A₁^/ в точку схода F₁^т, с перспективной проекцией светового луча, направленного из точки A^/ в точку схода F^т. Аналогичным образом строится тень от точки B, что позволяет построить тень от отрезка по двум точкам.

Тень от горизонтальной прямой AB на горизонтальную плоскость также является горизонтальной прямой A^тB^т, которая параллельна исходному отрезку AB, и следовательно, имеет ту же точку схода F. Тень от вертикальной прямой на горизонтальную плоскость совпадает с направлением вторичной проекции светового луча (рис.8.4).

На практике чаще всего используется первый случай направления световых лучей, т.к. большая часть объекта в этом случае освещена и перспектива выглядит наиболее выразительно.

Из всех способов построения теней, известных по теням на комплексном чертеже, в перспективе используются только два: способ лучевых сечений и способ обратных лучей. Остальные способы не используются, т.к. приводят к сложным построениям.

Последовательность построения теней такая же, как и на комплексном чертеже: выявляется контур собственной тени, затем строится падающая тень от контура собственной тени каждого геометрического образа на предметную плоскость (на комплексном чертеже на стену), затем падающие тени от одного геометрического образа на другой.

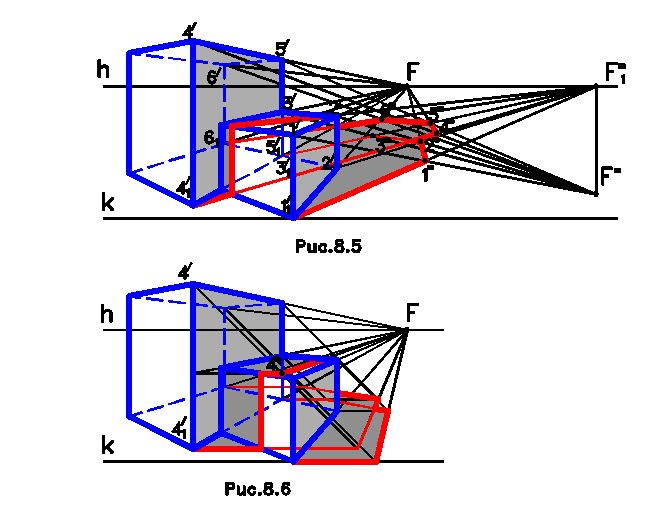
На рис.8.5 показано построение теней на примере двух параллелепипедов. От контура собственной тени 1^/ - 2^/ - 3^/ - 1₁^/ - 2₁^/ - 3₁^/ малого параллелепипеда построена тень на предметную плоскость как от вертикальных и горизонтальных прямых. Затем построена тень от контура собственной тени 4^/ - 5^/ - 6^/ - 4₁^/ - 5₁^/ - 6₁^/ большого параллелепипеда на предметную плоскость. Контуром падающей тени обоих параллелепипедов является огибающий контур обеих теней. Кроме того, тень от большого параллелепипеда падает на верхнюю горизонтальную и переднюю вертикальную грани малого параллелепипеда. Для этого строятся лучевые сечения малого параллелепипеда, полученные от пересечения лучевых плоскостей, проведенных через контур собственных теней большого параллелепипеда. Такая лучевая плоскость проведена через ребро 4^/ - 4₁^/ большого параллелепипеда, и она пересекла малый параллелепипед по сечению, которое является контуром падающей. Другие участки собственной тени большого параллелепипеда дают тени только на предметную плоскость. На рис.8.6 построены тени от тех же параллелепипедов при фронтальном положении лучей.