Решение. Из соображений симметрии, очевидно, что вектор напряженности электрического поля может быть направлен только радиально

Из соображений симметрии, очевидно, что вектор напряженности электрического поля может быть направлен только радиально. Законы изменения напряжённости поля с расстоянием от оси внутри и снаружи цилиндра могут различаться. Поэтому область 1– внутри цилиндра и область 2 – снаружи необходимо исследовать отдельно.

 

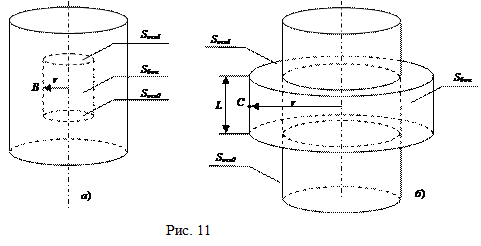
Для определения напряженности в произвольной точке В, находящейся внутри заданного цилиндра (рис. 11, а), выберем замкнутую поверхность в виде второго (вспомогательного) цилиндра радиусом r, ось которого совпадает с осью заданного цилиндра (цилиндры коаксиальные). Второй цилиндр имеет боковую поверхность S _бок и два основания S_осн1 и S_{осн 2}. Его радиус равен расстоянию от оси до точки В. Таким образом, точка В находится на боковой поверхности второго цилиндра. Зарядов внутри него нет.

В соответствии с теоремой Гаусса (3.1)

Интеграл по замкнутой поверхности S можно представить в виде суммы интегралов по основаниям и боковой поверхности

, (3.6)

Так как вектор напряженности направлен радиально, то скалярные произведения в первых двух интегралах равны нулю, а в последнем, .

Из соображения симметрии напряженности поля в точках, принадлежащих боковой поверхности, должны быть одинаковыми. Тогда равенство (3.6) примет вид

, (3.7)

Равенство (3.7) может иметь место только при выполнении условия Е = 0. Таким образом, в любой точке внутри заряженного по поверхности цилиндра напряженность электрического поля равна нулю.

Для определения напряженности в произвольной точке С, снаружи заданного цилиндра, аналогично выберем вспомогательную замкнутую поверхность в виде третьего коаксиального цилиндра высотой L (рис. 11, б). Его радиус равен расстоянию от точки С до оси заданного цилиндра. Так как внутри вспомогательной поверхности интегрирования находится заряд , то для нее теорема Гаусса имеет вид

, (3.8)

Интеграл в левой части этого равенства по аналогии с предыдущим случаем представим в виде суммы таких же трех интегралов, из которых ненулевым является только интеграл по боковой поверхности (рис. 2.10, б):

Последний интеграл равен площади боковой поверхности цилиндра S _6ок = 2π rL.

Из теоремы Гаусса получим

. (3.9)

Отсюда напряжённость электростатического поля

при . (3.10)

При r = R значение напряженность поля максимально

. (3.11)

Так как внутри цилиндра поле отсутствует, то разность потенциалов между осью и заданной точкой А равна разности потенциалов между поверхностью цилиндра и этой точкой

=

Вычисления

.

Ответ: график изменения напряженности электрического поля с расстоянием от оси цилиндра приведен на рис. 2.12, разность потенциалов между осью цилиндра и точкой А равна 12, 5 В

 

Пример 3.2. Система зарядов представляет собой ядро с положительным зарядом равным элементарному заряду и «облако» отрицательного заряда, объемная плотность которого изменяется с расстоянием от ядра по закону

, (3.12)

где R – радиус, численно равный первой боровской орбите электрона в атоме водорода (R = 0, 53∙ 10^–10 м); е – элементарный заряд (е = 1, 6∙ 10^–19 Кл); r - расстояние от центра ядра, м.

Найти напряженность электрического поля на расстоянии R от ядра.

 

Решение

Выберем замкнутую сферическую поверхность с радиусом, равным R и центром в ядре (размерами ядра можнопренебречь). Из соображений симметрии во всех точках этой поверхности вектор напряженности электрического поля одинаков по модулю и перпендикулярен к поверхности (рис.13). Поэтому теорему Гаусса () для выбранной поверхности S запишем в виде

, (3.13)

где Q - суммарный заряд, находящийся внутри выбранной сферы, т.е. положительный заряд ядра, равный е, и отрицательный заряд электронного «облака» Q _обл. Этот заряд определим интегрированием плотности отрицательного заряда электронного «облака» по внутреннему объему выбранной сферы. Тогда

. (3.14)

Учитывая сферическую симметрию, элемент объема dV можно представить в виде dV = 4p r²dr. Тогда

(3.15)

Выбор метода вычисления студент определяет самостоятельно. Можно использовать метод интегрирования по частям или воспользоваться математическими справочниками. В результате получим

Используя теорему Гаусса , и, учитывая, что интеграл в левой части равен площади поверхности сферы S = 4p R ² для напряжённости поля получим

.

Вычисления

» 3, 5∙ 10¹¹ В/м.

Ответ: напряженность электрического поля на расстоянии R от ядра равна 3, 5∙ 10¹¹ В/м.