Теоретические основы. При наличии определенной симметрии в расположении зарядов, в некоторых случаях для расчета напряженности электрического поля применяется теорема Гаусса:
При наличии определенной симметрии в расположении зарядов, в некоторых случаях для расчета напряженности электрического поля применяется теорема Гаусса:
Поток вектора напряженности в левой части выражения (3.1) вычисляется по любой наиболее удобной замкнутой поверхности S, а в правой части учтены только заряды Qi, заключенные внутри этой поверхности. При непрерывном распределении зарядов суммирование зарядов в правой части уравнения (3.1) заменяется интегрированием плотности электрического заряда ρ по объему V, охватываемому замкнутой поверхностью S:
Чтобы избежать затруднений связанных с выбором замкнутой поверхности S при использовании теоремы Гаусса, необходимо найти направление вектора В этом случае поток вектора напряженности через замкнутую поверхность можно представить как сумму поверхностных интегралов:
где вторая сумма равна нулю Напряжённость и потенциал связаны между собой следующими соотношениями
Потенциал электрического поля в заданной точке А определяется по известной функциональной зависимости
3.2. Примеры решения заданий для выполнения расчётно-графических работ Пример 3.1. На поверхности бесконечного полого цилиндра, радиусом R = 10 см равномерно распределен заряд с линейной плотностью τ = 1 нКл/м. 1. Построить график изменения напряженности электрического поля в зависимости от расстояния до оси цилиндра Е = Е (r). 2. Найти разность потенциалов между осью цилиндра и точкой А, находящейся на расстоянии d = 20 см от нее.
|

 , (3.1)
, (3.1)
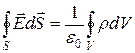 , (3.2)
, (3.2) в пространстве, окружающем заряженное тело из соображений симметрии. При этом точка, в которой определяют вектор напряженности, должна принадлежать замкнутой поверхности интегрирования S. Поверхность S выбирают симметричной расположению зарядов, а ее составные части должны быть либо перпендикулярны (Si), либо касательные к вектору напряженности (Sj).
в пространстве, окружающем заряженное тело из соображений симметрии. При этом точка, в которой определяют вектор напряженности, должна принадлежать замкнутой поверхности интегрирования S. Поверхность S выбирают симметричной расположению зарядов, а ее составные части должны быть либо перпендикулярны (Si), либо касательные к вектору напряженности (Sj). , (3.3)
, (3.3) , а первая преобразуется к виду
, а первая преобразуется к виду 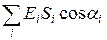 , где α i = 0 или α i = π.
, где α i = 0 или α i = π. или
или 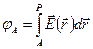 (3.4)
(3.4) . При этом принимают, что потенциал поля в точке Р равен нулю. Для точечных и сферически симметричных зарядов эту точку удобно располагать на бесконечности. Из формулы (2.17) следует разность потенциаловмежду двумя точками поля А и В
. При этом принимают, что потенциал поля в точке Р равен нулю. Для точечных и сферически симметричных зарядов эту точку удобно располагать на бесконечности. Из формулы (2.17) следует разность потенциаловмежду двумя точками поля А и В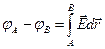 , (3.5)
, (3.5)


