Теоретические основы. В электростатике рассматриваются свойства и взаимодействия неподвижных в инерциальной системе отсчёта электрически заряженных тел или частиц
В электростатике рассматриваются свойства и взаимодействия неподвижных в инерциальной системе отсчёта электрически заряженных тел или частиц, обладающих электрическим зарядом. Электрический заряд это физическая величина, характеризующая свойство заряженных частиц или тел вступать в электромагнитные взаимодействия и определяющая величину сил и энергий при таких взаимодействиях. Все тела в природе способны электризоваться, т.е. приобретать электрический заряд. Наличие электрического заряда проявляется в том, что заряженное тело взаимодействует с другими заряженными телами. В природе существуют два вида электрических зарядов. Условно их называют положительными и отрицательными. Заряды одного знака отталкиваются, разных знаков – притягиваются друг к другу. Самым маленьким является заряд элементарных частиц. Этот заряд называется элементарным. Абсолютное значение элементарного заряда Если каким либо образом создать в теле избыток частиц одного знака, то тело окажется заряженным. Электрический заряд квантуется. Заряженное тело имеет заряд q, который равен целому числу элементарных зарядов, т.е. Заряд, сосредоточенный на теле, линейные размеры которого пренебрежимо малы по сравнению с расстоянием до других тел, с которыми он взаимодействует, называется точечным зарядом. Величина заряда, измеряемая в различных инерциальных системах отсчёта, оказывается одинаковой. Система называется электрически изолированной, если через ограничивающую её поверхность не могут проникать заряженные частицы. Закон сохранения электрического заряда. В электрически изолированной системе взаимодействующих заряженных тел, алгебраическая сумма электрических зарядов остаётся постоянной.
где: q i – i -ый заряд системы, Закон сохранения электрического заряда является фундаментальным и тесно связан с релятивистской инвариантностью заряда. Закон Кулона Закон Кулонасправедлив для взаимодействия неподвижных точечных зарядов, а также заряженных тел шарообразной формы, если их заряды равномерно распределены по всему объёму или по всей поверхности этих тел. Формулировка закона: сила взаимодействия между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам и обратно пропорциональна квадрату расстояния между ними
где Линейная плотность заряда
Поверхностная плотность заряда
Объёмная плотность заряда
где dq – элементарный заряд; d l, dS, dV – элементы длины, площади и объема. Электрическое поле. Всякий электрический заряд или заряженное тело изменяет свойства окружающего его пространства, создавая в нём электрическое поле. Электрическое поле проявляет себя в действии силы на электрический заряд, помещённый в какую-либо точку этого поля. Векторной силовой характеристикой электрического поля является напряжённость поля. Напряженность электрического поля
здесь q - заряд, помещенный в электрическом поле (пробный заряд). Пробный заряд должен быть настолько мал, чтобы он не мог исказить исследуемое с его помощью поле. Если q > 0, вектор Напряженность поля точечного заряда в вакууме
где Если q > 0, вектор
Однородное электрическое поле – поле, в каждой точке которого напряженность Если Поле точечного заряда – неоднородное. Принцип суперпозиции электрических полей: Напряженность электрического поля системы точечных зарядов в любой точке пространства равна геометрической сумме напряженностей полей каждого из этих зарядов в отдельности. Заряды в пространстве распределяются либо дискретно, либо непрерывно. · В случае дискретного распределения электрических зарядов:
· Напряженность поля в точке А, создаваемая двумя точечными зарядами q 1 и q 2, (см. рис.2) равна
где Модуль напряженности в случае суперпозиции двух полей
где α – угол между Е1 и Е2.
· Напряженность электростатического поля, создаваемого системой неподвижных точечных зарядов q 1, q 2, …, q n:
где Энергетической характеристикой электрического поля является потенциал поля
Потенциальная энергия поля точечного заряда
Потенциал электрического поля точечного заряда q на расстоянии r от него
Потенциал поля металлической сферы радиусом R, несущей заряд q на расстоянии r от центра
Связь напряженности и потенциала электрического поля
где grad φ – градиент потенциала.
Для сферической симметрии поля
1.2. Примеры решения заданий для выполнения расчётно-графических работ
Пример 1.1 Электрическое поле создано бесконечной плоскостью, заряженной с поверхностной плотностью σ = 400 нКл/м 2, и бесконечной прямой нитью, заряженной с линейной плотностью τ = 100 нКл/м. Нить расположена перпендикулярно плоскости. На расстоянии r = 10 см от нити находится точечный заряд q = 10 нКл. Определить силу, действующую на заряд.
Согласно принципу суперпозиции электрических полей (1.9), напряженность поля, в точке, где находится заряд q:
Поле, создаваемое плоскостью, однородно, и модуль напряженности в любой точке поля определяется по формуле:
Поле заряженной линии неоднородно и модуль его напряженности определяется по формуле:
Так как векторы
или
Используя формулу для силы (), получим
Проверка размерности
Вычисления
Ответ: сила, действующая на заряд, равна F = 289·10-6 Н.
Пример 1.2 В углах при основании равнобедренного треугольника с боковой стороной 8 см расположены заряды Q1 и Q2. Определить силу, действующую на заряд 1 нКл, помещенный в вершине треугольника. Угол при вершине 120°. Рассмотреть случаи: 1.Q1 = Q2 = 2 нКл 2.Q1 = - 2 нКл, Q2 = 2 нКл Дано:
|

 Кл. Устойчивыми частицами, которые входят в состав любого вещества, являются электрон (элементарный заряд отрицательный) и протон (элементарный заряд положительный).
Кл. Устойчивыми частицами, которые входят в состав любого вещества, являются электрон (элементарный заряд отрицательный) и протон (элементарный заряд положительный). , где N – число элементарных зарядов. [ N ]=безразмерная величина, [ q ]= Кл, [ e ]= Кл.
, где N – число элементарных зарядов. [ N ]=безразмерная величина, [ q ]= Кл, [ e ]= Кл. , (1.1)
, (1.1) Кл; п - число зарядов.
Кл; п - число зарядов. , (1.2)
, (1.2)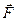 – сила взаимодействия зарядов q1 и q2; r расстояние между зарядами; ε о – электрическая постоянная, ε – диэлектрическая проницаемость среды;
– сила взаимодействия зарядов q1 и q2; r расстояние между зарядами; ε о – электрическая постоянная, ε – диэлектрическая проницаемость среды;  – орт-вектор направления действия силы.
– орт-вектор направления действия силы. , (1.3)
, (1.3) , (1.4)
, (1.4) , (1.5)
, (1.5) , (1.6)
, (1.6) направлен по
направлен по  , (1.7)
, (1.7) – радиус-вектор, соединяющий заряд q с точкой, в которой вычисляется напряженность поля; q – точечный заряд, создающий поле;
– радиус-вектор, соединяющий заряд q с точкой, в которой вычисляется напряженность поля; q – точечный заряд, создающий поле;  – электрическая постоянная.
– электрическая постоянная.

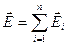 , (1.8)
, (1.8) где
где  – напряженность, создаваемая i -м зарядом в рассматриваемой точке поля, n – число дискретных зарядов, входящих в состав системы.
– напряженность, создаваемая i -м зарядом в рассматриваемой точке поля, n – число дискретных зарядов, входящих в состав системы. . (1.9)
. (1.9) – напряженность, создаваемая зарядом q 1 в точке А.
– напряженность, создаваемая зарядом q 1 в точке А.  – напряженность, создаваемая зарядом q 2 в точке А.
– напряженность, создаваемая зарядом q 2 в точке А. , (1.10)
, (1.10) , (1.11)
, (1.11) – радиус-вектор, проведенный из точечного заряда
– радиус-вектор, проведенный из точечного заряда  в рассматриваемую точку поля,
в рассматриваемую точку поля,  , (1.12)
, (1.12) . (1.13)
. (1.13) . (1.14)
. (1.14) ; (1.15)
; (1.15) . (1.16)
. (1.16) , (1.17)
, (1.17) . (1.18)
. (1.18) .
. . (1.20)
. (1.20) . (1.21)
. (1.21) , (1.22)
, (1.22) . (1.23)
. (1.23) . (1.24)
. (1.24) .
. .
. Кл;
Кл;  Кл; r = 0, 08 м; a = 30°; e = 1, F1 и F2 -?.
Кл; r = 0, 08 м; a = 30°; e = 1, F1 и F2 -?.


