Расчётно-графическая работа 4
Тема: вычисление полей с помощью теоремы Гаусса.
Формулировка задания.
Шар (цилиндр, пластина) радиусом (толщиной) R имеет положительный заряд Q, объемная плотность которого  зависит от расстояния r до его центра (до оси) по закону, указанному в таблице 2, в соответствии с номером варианта.
зависит от расстояния r до его центра (до оси) по закону, указанному в таблице 2, в соответствии с номером варианта.
Определите:
-напряженность электрического поля на поверхности шара (сферы, цилиндра);
-напряженность электрического поля на расстоянии r = R /2 от центра (от оси);
-потенциал электрического поля в центре шара (на оси);
-разность потенциалов между поверхностью и центром шара (осью цилиндра).
Постройте график зависимости напряженности поля Е = Е (r) от расстояния до центра шара.
Таблица 2. Значения параметров по вариантам. (Варианты 1 – 10)
| Номер
Варианта
| Заряженное тело
| Закон
| r 0
| R
|
| нКл/м3
| м
|
|
| шар
|  , Q = 92 e
(элементарный заряд е = 1, 6∙ 10− 19 Кл.) , Q = 92 e
(элементарный заряд е = 1, 6∙ 10− 19 Кл.)
|
| 10− 14
|
|
| шар
|  . a= 10 м3- . a= 10 м3-
|
|
|
|
| шар
| 
|
| 0, 1
|
|
| шар
|  , b= 1 мкКл/м , b= 1 мкКл/м
|
| 0, 1
|
|
| шар
|  . b= 1 мкКл/м . b= 1 мкКл/м
|
| 0, 1
|
|
| шар
| 
|
| 0, 1
|
|
| шар
| 
|
| 10-10
|
|
| цилиндр
| 
| 10
| 0, 1
|
|
| цилиндр
| 
|
| 0, 1
|
|
| пластина
| 
|
| 0.02
|
Таблица 3. Индивидуальные задания. Варианты 11 – 25
| Вариант
| Задание
|
|
| Пространство между двумя концентрическими сферами, радиусы которых R l = 10 см и R 2 = 20 см, заряжено с объемной плотностью  , где b =1 нКл/м, r - расстояние от центра сфер. Определите разность потенциалов между сферами. Постройте график зависимости напряженности электрического поля от расстояния до центра сфер. , где b =1 нКл/м, r - расстояние от центра сфер. Определите разность потенциалов между сферами. Постройте график зависимости напряженности электрического поля от расстояния до центра сфер.
|
|
| Шар радиусом R = 100 м имеет заряд Q = 10 нКл, однородно распределенный по его объему. Шар окружает среда, имеющая объемную плотность электрического заряда, зависящую от расстояния r до центра шара по закону  . Определите разность потенциалов между поверхностью шара и точкой, находящейся на расстоянии r = 2 R oт центра шара. Постройте график зависимости напряженности от расстояния до центра шара. . Определите разность потенциалов между поверхностью шара и точкой, находящейся на расстоянии r = 2 R oт центра шара. Постройте график зависимости напряженности от расстояния до центра шара.
|
|
| Шар, имеющий положительный заряд Q = 1 нКл, окружен симметрично отрицательным зарядом с объемной плотностью  , где b = -34, 6 нКл/м, R = 1 см - радиус шара, r - расстояние от центра шара. Определите напряженность электрического поля на расстоянии r = 2 R от центра шара. Постройте график зависимости напряженности поля от r. , где b = -34, 6 нКл/м, R = 1 см - радиус шара, r - расстояние от центра шара. Определите напряженность электрического поля на расстоянии r = 2 R от центра шара. Постройте график зависимости напряженности поля от r.
|
|
| Пространство между двумя коаксиальными длинными цилиндрами заполнено электрическим зарядом с объемной плотностью, изменяющейся по закону  , где b = 10 нКл/м. Радиусы цилиндров R 1 = 1 см, R 2 = 2 см. Определите разность потенциалов между цилиндрами. , где b = 10 нКл/м. Радиусы цилиндров R 1 = 1 см, R 2 = 2 см. Определите разность потенциалов между цилиндрами.
|
|
| Длинный цилиндр радиусом R = 10 см заряжен так, что объемная плотность электрического заряда r изменяется с расстоянием r от оси по закону  , где r0 = 10 нКл/м3. Определите напряженность электрического поля в точке, находящейся на расстоянии , где r0 = 10 нКл/м3. Определите напряженность электрического поля в точке, находящейся на расстоянии  от оси. Постройте график зависимости напряженности поля от r. от оси. Постройте график зависимости напряженности поля от r.
|
|
| Длинный цилиндр радиусом R = 2 см несет заряд, равномерно распределенный по его объему с плотностью r = 10 нКл/м3. Определите разность потенциалов между точками, отстоящими от оси цилиндра на расстояниях r 1 = 1 см и r 2 = 3 см. Постройте график зависимости напряженности от расстояния до оси цилиндра.
|
|
| Длинная нить имеет положительный заряд с линейной плотностью t = 10 нКл/м. Радиус нити R = 1 мм. Среда, окружающая нить, имеет объемную плотность положительного заряда, изменяющуюся в зависимости от расстояния от оси нити r по закону 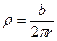 , где b = 10 мкКл/м2. Определите разность потенциалов между поверхностью нити и точкой, отстоящей от ее оси на расстоянии r = 11 R. Постройте график зависимости напряженности от расстояния до оси нити. , где b = 10 мкКл/м2. Определите разность потенциалов между поверхностью нити и точкой, отстоящей от ее оси на расстоянии r = 11 R. Постройте график зависимости напряженности от расстояния до оси нити.
|
|
| Длинная тонкая нить имеет положительный заряд линейной плотностью t = 10 нКл/м. Среда, окружающая нить, имеет заряд другого знака с объемной плотностью, зависящей только от расстояния r до нити по закону  , где r 0 = -100нКл/м3, R = 10 см. Определите напряженность электрического поля на расстоянии R от нити. Постройте график зависимости напряженности от r. , где r 0 = -100нКл/м3, R = 10 см. Определите напряженность электрического поля на расстоянии R от нити. Постройте график зависимости напряженности от r.
|
|
| Пространство вблизи прямой длинной нити накала электронной лампы заряжено отрицательным зарядом с объемной плотностью  , где R = 0, 1 мм - радиус нити, b = - 4, 3 мкКл/м2, r - расстояние от оси нити. Сама нить заряжена положительным зарядом линейной плотностью t = 1 нКл/м. Определите напряженность электрического поля на расстоянии r = 2R от оси нити. Постройте график зависимости напряженности поля, от r. , где R = 0, 1 мм - радиус нити, b = - 4, 3 мкКл/м2, r - расстояние от оси нити. Сама нить заряжена положительным зарядом линейной плотностью t = 1 нКл/м. Определите напряженность электрического поля на расстоянии r = 2R от оси нити. Постройте график зависимости напряженности поля, от r.
|
|
| Пластина толщиной d = 2 см имеет электрический заряд, распределенный так, что его объемная плотность зависит только от координаты х, перпендикулярной толщине пластины, по закону  , где r 0 = 10 нКл/м3, Определите разность потенциалов между центром и краем пластины, считая ее плоскость бесконечной. Постройте график зависимости напряженности поля от координаты х. , где r 0 = 10 нКл/м3, Определите разность потенциалов между центром и краем пластины, считая ее плоскость бесконечной. Постройте график зависимости напряженности поля от координаты х.
|
|
| Бесконечная пластина толщиной d = 10 см имеет заряд, объемная плотность которого изменяется по закону  , где r 0 = 10 нКл/м3, | х | - расстояние от центра пластины в поперечном направлении. Определите разность потенциалов между центром пластины и ее поверхностью. Постройте график зависимости Е = Е (х). , где r 0 = 10 нКл/м3, | х | - расстояние от центра пластины в поперечном направлении. Определите разность потенциалов между центром пластины и ее поверхностью. Постройте график зависимости Е = Е (х).
|
|
| Тонкая пластина равномерно заряжена так, что на единицу площади ее поверхности приходится заряд s = 1 нКл/м2. Среда вблизи пластины имеет заряд другого знака с объемной плотностью, зависящей от расстояния х до пластины по закону 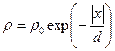 , где r 0 = 10 нКл/м3, d = 10 см. На каком расстоянии от пластины напряженность электрического поля равна нулю? Чему равна разность потенциалов между этой точкой и пластиной? , где r 0 = 10 нКл/м3, d = 10 см. На каком расстоянии от пластины напряженность электрического поля равна нулю? Чему равна разность потенциалов между этой точкой и пластиной?
|
|
| Большая плоская пластина толщиной d = 4 см имеет положительный заряд, равномерно распределенный по объему с объемной плотностью r = 10 нКл/м3. Определитеразность потенциалов между поверхностью и точкой, находящейся внутри пластины на расстоянии b = 1 см от поверхности. Постройте график зависимости напряженности от расстояния до центра пластины.
|
|
| Пространство между двумя параллельными бесконечными плоскостями заполнено зарядом. Расстояние между плоскостями d = 1 см. Если принять, что координатная плоскость (уz)находится посередине между плоскостями, то объемную плотность электрического заряда можно записать как функцию 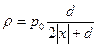 , где r 0 = 1 мкКл/м3. Определите разность потенциалов между точкой, имеющей координату х = d, и ближайшей поверхностью пластины. Постройте график зависимости напряженности от координаты х. , где r 0 = 1 мкКл/м3. Определите разность потенциалов между точкой, имеющей координату х = d, и ближайшей поверхностью пластины. Постройте график зависимости напряженности от координаты х.
|
|
| Пространство вблизи тонкой бесконечной плоской незаряженной пластины имеет электрический заряд, распределенный симметрично пластине с объемной плотностью  , где b = 1 см, r 0 = 1 мкКл/м3, | x | - расстояние от пластины. Определите разность потенциалов между пластиной и точкой, находящейся на расстоянии b от нее. Постройте график зависимости напряженности от х. , где b = 1 см, r 0 = 1 мкКл/м3, | x | - расстояние от пластины. Определите разность потенциалов между пластиной и точкой, находящейся на расстоянии b от нее. Постройте график зависимости напряженности от х.
|
Расчётно-графическая работа 5
Тема: определение характеристик поля системы заряженныхкоаксиальных длинных цилиндров, с помощью теоремы Гаусса.
Формулировка задания. (Варианты 1-12)
На рис.15 приведена система заряженных коаксиальных длинных цилиндров. Линейные плотности зарядов на цилиндрах приведены в таблице 5.Радиусы цилиндров соответственно R1 = 10см, R2 = 20 см, R3 = 30 см, R4 = 40 см.
1. Постройте график зависимости напряженности электрического поля от расстояния до оси цилиндров.
2. Определите разность потенциалов между внутренним и внешним цилиндрами.
 Таблица 5. Значения параметров по вариантам.
Таблица 5. Значения параметров по вариантам.
| Номер задания
| Линейные плотности зарядов на цилиндрах, нКл/м
|

| 
| 
| 
|
|
|
|
|
| -10
|
|
|
|
| -10
|
|
|
|
|
| -10
| -10
|
|
|
| -10
|
| -10
|
|
|
| -20
|
|
|
|
|
|
| -10
|
|
|
|
| -10
|
|
|
|
| -10
|
|
|
|
|
| -10
|
| -10
|
|
|
| -10
|
|
| -10
|
|
|
|
| -20
|
|
|
|
|
| -20
|
|
Тема: определение характеристик поля системы заряженных концентрических сфер, с помощью теоремы Гаусса.
Формулировка задания. (Варианты 13 – 25)
На рис. 14 приведена система заряженных концентрических сфер. Радиусы сфер соответственно R1= 10 см, R2= 20см, R3 = 30 см, R4 = 40 см. Величины зарядов сфер Q1 указаны в таблице 6 в соответствии с вариантом.
1. Постройте график зависимости напряженности электрического поля от расстояния до центра сфер Е = Е(r).
2. Определите разность потенциалов между внутренней и внешней сферами  .
.
Таблица 6. Значения параметров по вариантам.
| Номер задания
| Заряды на сферах, нКл
|
| Q1
| Q2
| Q3
| Q4
|
|
|
|
|
| -10
|
|
|
|
| -10
|
|
|
|
|
| -10
| -10
|
|
|
| -10
|
| -10
|
|
|
| -20
|
|
|
|
|
|
| -10
|
|
|
|
| -10
|
|
|
|
| -10
|
|
|
|
|
| -10
|
| -10
|
|
| 10.
| -10
|
|
| -10
|
|
|
|
| -20
|
|
|
|
|
| -20
|
|
|
| -20
|
| -10
|
|
IV. ЭЛЕКТРОЁМКОСТЬ. КОНДЕНСАТОРЫ

 зависит от расстояния r до его центра (до оси) по закону, указанному в таблице 2, в соответствии с номером варианта.
зависит от расстояния r до его центра (до оси) по закону, указанному в таблице 2, в соответствии с номером варианта. , Q = 92 e
(элементарный заряд е = 1, 6∙ 10− 19 Кл.)
, Q = 92 e
(элементарный заряд е = 1, 6∙ 10− 19 Кл.)
 . a= 10 м3-
. a= 10 м3-

 , b= 1 мкКл/м
, b= 1 мкКл/м
 . b= 1 мкКл/м
. b= 1 мкКл/м





 , где b =1 нКл/м, r - расстояние от центра сфер. Определите разность потенциалов между сферами. Постройте график зависимости напряженности электрического поля от расстояния до центра сфер.
, где b =1 нКл/м, r - расстояние от центра сфер. Определите разность потенциалов между сферами. Постройте график зависимости напряженности электрического поля от расстояния до центра сфер.
 . Определите разность потенциалов между поверхностью шара и точкой, находящейся на расстоянии r = 2 R oт центра шара. Постройте график зависимости напряженности от расстояния до центра шара.
. Определите разность потенциалов между поверхностью шара и точкой, находящейся на расстоянии r = 2 R oт центра шара. Постройте график зависимости напряженности от расстояния до центра шара.
 , где b = -34, 6 нКл/м, R = 1 см - радиус шара, r - расстояние от центра шара. Определите напряженность электрического поля на расстоянии r = 2 R от центра шара. Постройте график зависимости напряженности поля от r.
, где b = -34, 6 нКл/м, R = 1 см - радиус шара, r - расстояние от центра шара. Определите напряженность электрического поля на расстоянии r = 2 R от центра шара. Постройте график зависимости напряженности поля от r.
 , где r0 = 10 нКл/м3. Определите напряженность электрического поля в точке, находящейся на расстоянии
, где r0 = 10 нКл/м3. Определите напряженность электрического поля в точке, находящейся на расстоянии  от оси. Постройте график зависимости напряженности поля от r.
от оси. Постройте график зависимости напряженности поля от r.
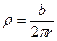 , где b = 10 мкКл/м2. Определите разность потенциалов между поверхностью нити и точкой, отстоящей от ее оси на расстоянии r = 11 R. Постройте график зависимости напряженности от расстояния до оси нити.
, где b = 10 мкКл/м2. Определите разность потенциалов между поверхностью нити и точкой, отстоящей от ее оси на расстоянии r = 11 R. Постройте график зависимости напряженности от расстояния до оси нити.
 , где r 0 = -100нКл/м3, R = 10 см. Определите напряженность электрического поля на расстоянии R от нити. Постройте график зависимости напряженности от r.
, где r 0 = -100нКл/м3, R = 10 см. Определите напряженность электрического поля на расстоянии R от нити. Постройте график зависимости напряженности от r.
 , где R = 0, 1 мм - радиус нити, b = - 4, 3 мкКл/м2, r - расстояние от оси нити. Сама нить заряжена положительным зарядом линейной плотностью t = 1 нКл/м. Определите напряженность электрического поля на расстоянии r = 2R от оси нити. Постройте график зависимости напряженности поля, от r.
, где R = 0, 1 мм - радиус нити, b = - 4, 3 мкКл/м2, r - расстояние от оси нити. Сама нить заряжена положительным зарядом линейной плотностью t = 1 нКл/м. Определите напряженность электрического поля на расстоянии r = 2R от оси нити. Постройте график зависимости напряженности поля, от r.
 , где r 0 = 10 нКл/м3, Определите разность потенциалов между центром и краем пластины, считая ее плоскость бесконечной. Постройте график зависимости напряженности поля от координаты х.
, где r 0 = 10 нКл/м3, Определите разность потенциалов между центром и краем пластины, считая ее плоскость бесконечной. Постройте график зависимости напряженности поля от координаты х.
 , где r 0 = 10 нКл/м3, | х | - расстояние от центра пластины в поперечном направлении. Определите разность потенциалов между центром пластины и ее поверхностью. Постройте график зависимости Е = Е (х).
, где r 0 = 10 нКл/м3, | х | - расстояние от центра пластины в поперечном направлении. Определите разность потенциалов между центром пластины и ее поверхностью. Постройте график зависимости Е = Е (х).
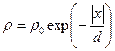 , где r 0 = 10 нКл/м3, d = 10 см. На каком расстоянии от пластины напряженность электрического поля равна нулю? Чему равна разность потенциалов между этой точкой и пластиной?
, где r 0 = 10 нКл/м3, d = 10 см. На каком расстоянии от пластины напряженность электрического поля равна нулю? Чему равна разность потенциалов между этой точкой и пластиной?
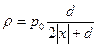 , где r 0 = 1 мкКл/м3. Определите разность потенциалов между точкой, имеющей координату х = d, и ближайшей поверхностью пластины. Постройте график зависимости напряженности от координаты х.
, где r 0 = 1 мкКл/м3. Определите разность потенциалов между точкой, имеющей координату х = d, и ближайшей поверхностью пластины. Постройте график зависимости напряженности от координаты х.
 , где b = 1 см, r 0 = 1 мкКл/м3, | x | - расстояние от пластины. Определите разность потенциалов между пластиной и точкой, находящейся на расстоянии b от нее. Постройте график зависимости напряженности от х.
, где b = 1 см, r 0 = 1 мкКл/м3, | x | - расстояние от пластины. Определите разность потенциалов между пластиной и точкой, находящейся на расстоянии b от нее. Постройте график зависимости напряженности от х.

 Таблица 5. Значения параметров по вариантам.
Таблица 5. Значения параметров по вариантам.



 .
.


