Характеристическое уравнение АС получаем из передаточной функции системы (по знаменателю уравнения (9)):
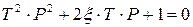 .
.
И хотя величина  , не определена, из выражений (11) и (12) для коэффициентов уравнения
, не определена, из выражений (11) и (12) для коэффициентов уравнения 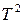 и
и  следует, что при любых
следует, что при любых  , коэффициенты уравнений положительны (заметим, что при
, коэффициенты уравнений положительны (заметим, что при  характеристическое уравнение АС становится уравнением первой степени). В соответствии с критерием устойчивости Гурвица-Рауса это является необходимым и достаточным условием устойчивости АС с характеристическим уравнением второй степени.
характеристическое уравнение АС становится уравнением первой степени). В соответствии с критерием устойчивости Гурвица-Рауса это является необходимым и достаточным условием устойчивости АС с характеристическим уравнением второй степени.
ВЫБОР ПОСТОЯННОЙ ВРЕМЕНИ СЕРВОПРИВОДА 
Сервопривод в составе АС расположен в цепях обратных связей. Это обстоятельство свидетельствует о том, что его быстродействие, оцениваемое по постоянной времени  , не всегда способствует увеличению быстродействия АС в целом. Действительно, если допустить мгновенное быстродействие сервопривода, при котором
, не всегда способствует увеличению быстродействия АС в целом. Действительно, если допустить мгновенное быстродействие сервопривода, при котором  , то характеристическое уравнение становится уравнением первой степени:
, то характеристическое уравнение становится уравнением первой степени:
 ;
; 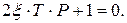
При этом неопределенность  раскрывается просто из выражения (12):
раскрывается просто из выражения (12):

т.е.  является определенной конечной величиной. Характеристическое уравнение при
является определенной конечной величиной. Характеристическое уравнение при  соответствует апериодическому звену, которое отличается наиболее низким быстродействием. Увеличение
соответствует апериодическому звену, которое отличается наиболее низким быстродействием. Увеличение  способствует снижению величины коэффициента затухания колебаний
способствует снижению величины коэффициента затухания колебаний  , и хотя в исследуемой АС невозможно получить характеристическое уравнение колебательного звена (
, и хотя в исследуемой АС невозможно получить характеристическое уравнение колебательного звена ( < 1) но, снижая
< 1) но, снижая  , можно достигнуть требуемой степени перерегулирования (в отличие от простого апериодического процесса) и существенно повысить быстродействие АС. Для этого амплитудно-частотная характеристика (АЧХ) АС должна иметь экстремум и, следовательно, частоту среза, отличную от нуля (
, можно достигнуть требуемой степени перерегулирования (в отличие от простого апериодического процесса) и существенно повысить быстродействие АС. Для этого амплитудно-частотная характеристика (АЧХ) АС должна иметь экстремум и, следовательно, частоту среза, отличную от нуля ( > 0).
> 0).
Возможность получения АЧХ с экстремумом видна на логарифмической АЧХ (ЛАЧХ) системы (рис.13). Передаточная функция АС

выражает последовательное соединение форсирующего и колебательного звеньев, поэтому с учетом частот излома  и
и  ЛАЧХ имеет излом асимптот при этой частоте АЧХ имеет значение амплитуды, близкое к максимальному.
ЛАЧХ имеет излом асимптот при этой частоте АЧХ имеет значение амплитуды, близкое к максимальному.
Чтобы получить эту величину, следует в выражении подставить значение частоты  .
.



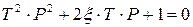 .
. , не определена, из выражений (11) и (12) для коэффициентов уравнения
, не определена, из выражений (11) и (12) для коэффициентов уравнения 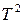 и
и  следует, что при любых
следует, что при любых  характеристическое уравнение АС становится уравнением первой степени). В соответствии с критерием устойчивости Гурвица-Рауса это является необходимым и достаточным условием устойчивости АС с характеристическим уравнением второй степени.
характеристическое уравнение АС становится уравнением первой степени). В соответствии с критерием устойчивости Гурвица-Рауса это является необходимым и достаточным условием устойчивости АС с характеристическим уравнением второй степени. ;
; 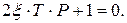
 раскрывается просто из выражения (12):
раскрывается просто из выражения (12):
 является определенной конечной величиной. Характеристическое уравнение при
является определенной конечной величиной. Характеристическое уравнение при  , и хотя в исследуемой АС невозможно получить характеристическое уравнение колебательного звена (
, и хотя в исследуемой АС невозможно получить характеристическое уравнение колебательного звена ( > 0).
> 0).
 и
и  ЛАЧХ имеет излом асимптот при этой частоте АЧХ имеет значение амплитуды, близкое к максимальному.
ЛАЧХ имеет излом асимптот при этой частоте АЧХ имеет значение амплитуды, близкое к максимальному. .
.




