
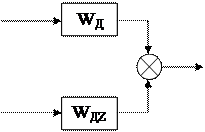
1. ДВС. Из структурной схемы ДВС (рис. 5) следует, что частота вращения первичного вала w
1 зависит от двух внешних воздействий:
– нагрузки на первичном валу и
– перемещения рейки топливного насоса ДВС, изменяющего количество топлива, подаваемого в двигатель.
Следовательно, ДВС имеет две передаточные функции:
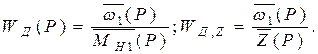
 Для получения передаточных функций запишем уравнение движения для ДВС, где искомой (выходной) функцией является управляемая величина – отклонение частоты вращения первичного вала
Для получения передаточных функций запишем уравнение движения для ДВС, где искомой (выходной) функцией является управляемая величина – отклонение частоты вращения первичного вала  от установившегося значения
от установившегося значения  :
:
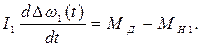
Момент сил ДВС по статической характеристике зависит от двух параметров: 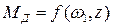 , следовательно,
, следовательно,
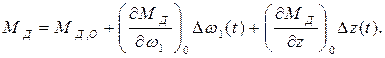
Запишем МН1(t) = МН1, 0 + Δ МН1(t). Заметив, что однородные параметры установившегося состояния равны, т. е. 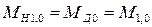 , и что
, и что
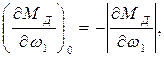
получим 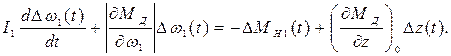
Введем в рассмотрение безразмерные функции времени для всех функций изменения во времени физических величин:
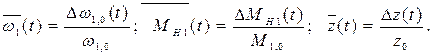
Получим дифференциальное уравнение ДВС для безразмерных функций времени:
где постоянные коэффициенты уравнения:
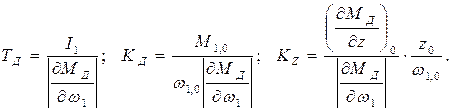
Здесь 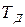 – постоянная времени двигателя, с;
– постоянная времени двигателя, с; 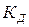 и
и  – безразмерные коэффициенты усиления.
– безразмерные коэффициенты усиления.
После перехода к изображениям получим две передаточные функции ДВС:
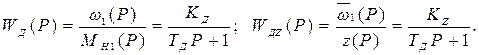
Так как в рассматриваемом числовом примере оценивается только один режим управления - при полной подаче топлива, то рейка насоса неподвижна и для оценки динамики АС понадобится только одна передаточная функция 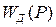 .
.
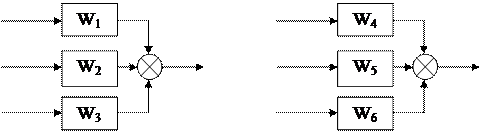
2. Бесступенчатая передача. Ее структурная схема характеризуется двумя управляемыми величинами, выходными воздействиями: нагрузкой, передаваемой через бесступенчатую передачу в ДВС, и скоростью, изменение которой воздействует, в свою очередь, на массу машины, вызывая нагрузки вторичного вала трансмиссии. Поэтому одна бесступенчатая передача в АС представлена двумя элементами, структурные схемы которых показаны на рис.6.
Изменение выходных воздействий зависит каждое от трех возмущений:
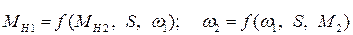
и, следовательно, каждый элемент характеризуется тремя передаточными функциями. Смысл передаточных функций 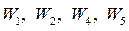 понятен, т.к. регулируемые величины меняются при изменении однородных возмущений и при перемещении органа управления передачей
понятен, т.к. регулируемые величины меняются при изменении однородных возмущений и при перемещении органа управления передачей  . Так, например, изменение
. Так, например, изменение 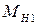 вызывается как изменением нагрузки на вторичном валу
вызывается как изменением нагрузки на вторичном валу 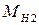 , так и изменением передаточного числа бесступенчатой передачи при перемещении
, так и изменением передаточного числа бесступенчатой передачи при перемещении  органа управления.
органа управления.

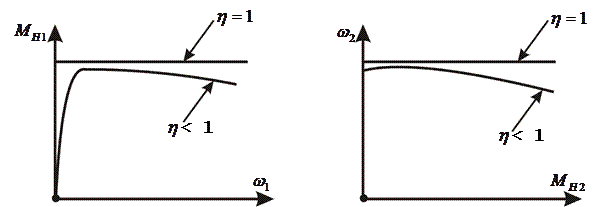
Зависимости 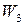 и
и  определяются КПД бесступенчатой передачи, как показано на рис. 7. Из рис. 7, а следует, что при очень малых частотах вращения вала гидрообъёмной бесступенчатой передачи из-за внутренних утечек масла невозможно поднять момент нагрузки на ее входном валу; при больших частотах вращения входного вала момент нагрузки также снижается из-за неудовлетворительной динамики поршневой группы и кавитационных явлений в цилиндрах поршневого блока. В связи с аналогичными причинами происходит снижение
определяются КПД бесступенчатой передачи, как показано на рис. 7. Из рис. 7, а следует, что при очень малых частотах вращения вала гидрообъёмной бесступенчатой передачи из-за внутренних утечек масла невозможно поднять момент нагрузки на ее входном валу; при больших частотах вращения входного вала момент нагрузки также снижается из-за неудовлетворительной динамики поршневой группы и кавитационных явлений в цилиндрах поршневого блока. В связи с аналогичными причинами происходит снижение 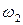 при увеличении
при увеличении 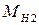 (рис.7, б).
(рис.7, б).
Если в приближенных расчетах пренебречь влияниями КПД бесступенчатой передачи, то передаточные функции 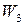 и
и  исчезают.
исчезают.
В соответствии с общими зависимостями составляем их аналитические (линеаризованные) выражения для каждого элемента: 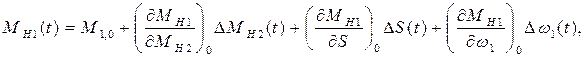
причем 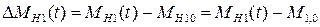 .
.


Обозначим безразмерные функции времени:
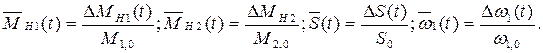
Получаем три передаточные функции для первого элемента:

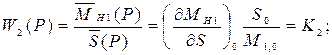
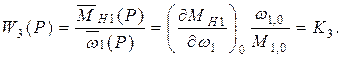
Если для первых приближенных оценок АС считать КПД бесступенчатой передачи равным единице и допустить прямую пропорциональность между перемещением органа управления  и изменением момента нагрузки
и изменением момента нагрузки 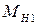 , то
, то
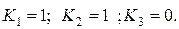
Аналогично получим передаточные функции второго элемента бесступенчатой передачи:
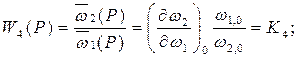
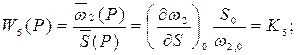
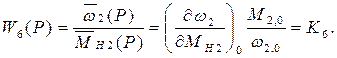
Здесь также, в приближенном выражении, при сделанных для первого элемента допущениях 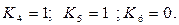
В приближенном изложении изменится и структурная схема бесступенчатой передачи (рис.6) для каждого элемента и будет соответствовать рис. 8.
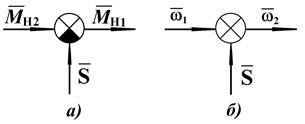

3. Транспортная самоходная машина. Управляемой выходной величиной является нагрузка на вторичном валу  , возмущениями – момент дорожных сопротивлений
, возмущениями – момент дорожных сопротивлений  и скорость вторичного вала
и скорость вторичного вала 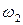 , изменению которой сопротивляется масса машины, вызывая нагрузки вторичного вала.
, изменению которой сопротивляется масса машины, вызывая нагрузки вторичного вала.
Для получения передаточной функции машины воспользуемся уравнением движения
Момент сопротивления
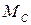
зависит от относительных дорожных сопротивлений
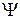
и скорости перемещения машины, т.е. от угловой скорости вращения вала вторичного
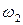
С увеличением
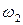
, растет ветровое сопротивление, а главное для гусеничной машины – потери в гусеничном движителе. Поэтому
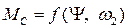
, что в линеаризованном виде соответствует выражению
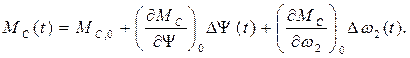
При этом 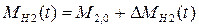 и
и 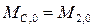 .
.
Обозначим безразмерные функции времени:
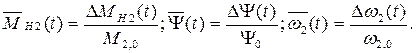
После этого дифференциальное уравнение машины приобретает вид
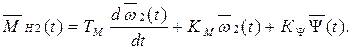
После перехода к изображениям получаем передаточные функции:
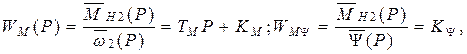
(3)
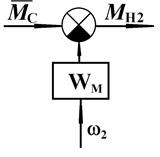 где
где 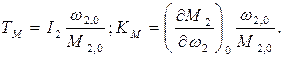
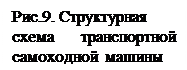 Величину
Величину 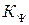 можно не определять аналитически, т.к. она характеризует нагрузку со стороны дороги и задается впоследствии независимо в виде типовых возмущений. Из выражения (3) уточняется структурная схема самоходной машины (рис.9). Из нее, в частности, следует, что нагрузка от дорожных сопротивлении
можно не определять аналитически, т.к. она характеризует нагрузку со стороны дороги и задается впоследствии независимо в виде типовых возмущений. Из выражения (3) уточняется структурная схема самоходной машины (рис.9). Из нее, в частности, следует, что нагрузка от дорожных сопротивлении 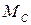 сразу и непосредственно нагружает вторичный вал машины
сразу и непосредственно нагружает вторичный вал машины 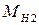 , а изменение скорости вторичного вала
, а изменение скорости вторичного вала 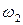 , воздействуя на массу машины
, воздействуя на массу машины 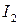 , создает нагрузку на валу машины с участием коэффициентов
, создает нагрузку на валу машины с участием коэффициентов  и
и  . Так как определение коэффициента
. Так как определение коэффициента  могло бы потребовать дополнительного построения статической характеристики
могло бы потребовать дополнительного построения статической характеристики 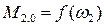 , то удобнее преобразовать выражение
, то удобнее преобразовать выражение  Проделаем такое преобразование:
Проделаем такое преобразование:  .
.
Значение 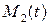 , в отличие от
, в отличие от  , переменно, с ростом
, переменно, с ростом 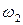 снижается КПД гусеничного движителя, и значение
снижается КПД гусеничного движителя, и значение  увеличивается в пропорции
увеличивается в пропорции 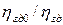 , т. е.
, т. е. 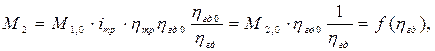
следовательно, 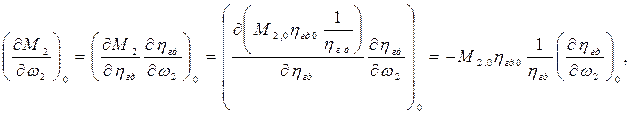
причем, 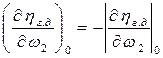 ;
;
тогда окончательно:
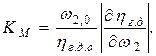 (4)
(4)
Теперь значение частной производной по графику  , приведенному в материалах по тяговому расчету машины и по статической характеристике АС (рис.3). Если в материалах тягового расчета машины
, приведенному в материалах по тяговому расчету машины и по статической характеристике АС (рис.3). Если в материалах тягового расчета машины 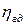 задан аналитически, математической аппроксимацией,
задан аналитически, математической аппроксимацией, 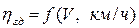 , то следует заменить в ней
, то следует заменить в ней 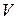 , используя
, используя 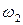 и переводной коэффициент в систему СИ, т.е.
и переводной коэффициент в систему СИ, т.е.  и определить частную производную
и определить частную производную 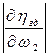 аналитически.
аналитически.
 4. Регулятор центробежный. Регулируемой, выходной величиной является перемещение
4. Регулятор центробежный. Регулируемой, выходной величиной является перемещение 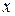 скользящей втулки регулятора, приводящее к перемещению рычага сервопривода. Возмущением является изменение скорости первичного вала
скользящей втулки регулятора, приводящее к перемещению рычага сервопривода. Возмущением является изменение скорости первичного вала 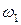 . Структурная схема центробежного регулятора показана на рис.10. Составим уравнение движения для скользящей втулки регулятора:
. Структурная схема центробежного регулятора показана на рис.10. Составим уравнение движения для скользящей втулки регулятора:
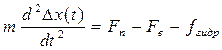 .
.
Здесь кроме поддерживающей силы от действия центробежных сил грузовых звеньев 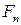 и восстанавливающей силы пружины
и восстанавливающей силы пружины 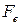 введена сила гидравлического трения скользящей втулки
введена сила гидравлического трения скользящей втулки
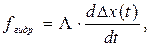
где 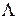 – коэффициент демпфирования;
– коэффициент демпфирования;  – масса всех деталей, в том числе и грузовых звеньев регулятора, приведенная к скользящей втулке. Значение поддерживающей и восстанавливающей сил:
– масса всех деталей, в том числе и грузовых звеньев регулятора, приведенная к скользящей втулке. Значение поддерживающей и восстанавливающей сил:
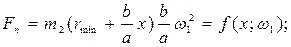
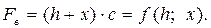
Их линеаризованные выражения:
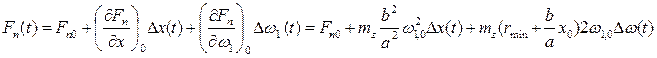
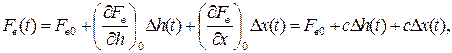
причем, 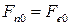 .
.
Преобразуем теперь уравнение движения звеньев регулятора:
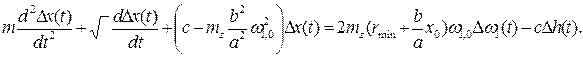
Введём безразмерные функции времени:
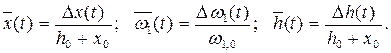
Получаем дифференциальное уравнение движения звеньев регулятора:
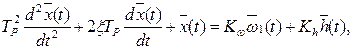
где 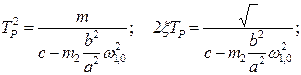
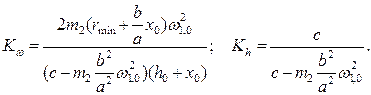 (5)
(5)
После перехода к изображениям функций получаем передаточные функции регулятора:
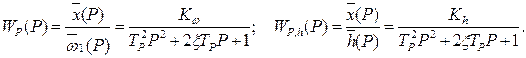
Так как в рассматриваемом примере машина работает с использованием максимальной мощности ДВС, то настройка  регулятора постоянна и регулятор описывается одной передаточной функцией
регулятора постоянна и регулятор описывается одной передаточной функцией
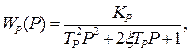
где 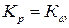 .
.
Оценим величину постоянной времени регулятора (см. формулу 5, с. 29) в соответствии с определенными ранее параметрами центробежного регулятора:
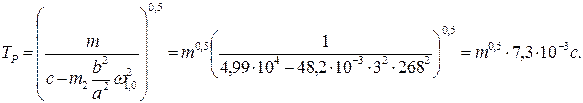
Так как постоянная времени регулятора  на несколько порядков меньше времени процессов управления АС, то можно рассматривать регулятор как пропорциональное звено, т.е., принимая
на несколько порядков меньше времени процессов управления АС, то можно рассматривать регулятор как пропорциональное звено, т.е., принимая 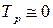 , можно полагать
, можно полагать 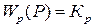 . Более удобно для расчетов
. Более удобно для расчетов  выражение
выражение 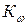 из (5) преобразовать следующим образом:
из (5) преобразовать следующим образом:
 (6)
(6)
причем при 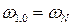

при 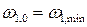
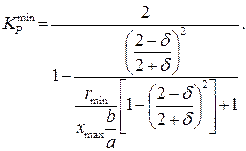
Величина 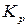 по параметрам заданий на проектирование АС меняется в пределах
по параметрам заданий на проектирование АС меняется в пределах 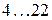 . Бó льшие значения
. Бó льшие значения 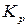 получаются при малых величинах
получаются при малых величинах 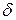 .
.
5. Гидросервопривод. Управляемой, выходной величиной в гидросервоприводе с жёсткой обратной связью является перемещение поршня  , связанного с органом управления бесступенчатой передачей. Возмущение создается перемещениям точки рычага жёсткой обратной связи, связанной со скользящей втулкой регулятора (см. рис.2 и 11). Гидросервопривод без жёсткой обратной связи, сам по себе, является классическим интегрирующим звеном с передаточной функцией
, связанного с органом управления бесступенчатой передачей. Возмущение создается перемещениям точки рычага жёсткой обратной связи, связанной со скользящей втулкой регулятора (см. рис.2 и 11). Гидросервопривод без жёсткой обратной связи, сам по себе, является классическим интегрирующим звеном с передаточной функцией

где 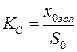 – отношение номинальных (нулевых) значений перемещений золотника и поршня, т. е. отношение их представляющих параметров, постоянная времени сервопривода:
– отношение номинальных (нулевых) значений перемещений золотника и поршня, т. е. отношение их представляющих параметров, постоянная времени сервопривода:
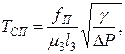
 где
где  – площадь поршня, м3;
– площадь поршня, м3;
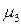 – коэффициент расхода жидкости через золотники,
– коэффициент расхода жидкости через золотники,  ;
;
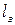 – ширина окна золотникового отверстия, м;
– ширина окна золотникового отверстия, м;
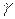 – плотность рабочей жидкости, Н/м3;
– плотность рабочей жидкости, Н/м3;
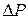 – суммарный перепад давлений, заставляющий поршень перемещаться, Па.
– суммарный перепад давлений, заставляющий поршень перемещаться, Па.
Очевидно, что постоянная времени  определяется практически соотношением площади поршня и проходного сечения золотника.
определяется практически соотношением площади поршня и проходного сечения золотника.
Гидросервопривод, охваченный жёсткой отрицательной обратной связью, становится апериодическим звеном [4] с передаточной функцией (см. рис. 11):
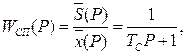
где 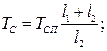
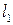 – расстояние между осями золотника и поршня;
– расстояние между осями золотника и поршня;
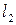 – расстояние между осями золотника и скользящей муфты регулятора.
– расстояние между осями золотника и скользящей муфты регулятора.
Задачей работы является обеспечение максимального быстродействия АС. Решение этой задачи следует производить определением такой величины 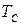 , которая обеспечит минимальное время
, которая обеспечит минимальное время  переходного процесса
переходного процесса  исследуемой АС.
исследуемой АС.
 1. ДВС. Из структурной схемы ДВС (рис. 5) следует, что частота вращения первичного вала w1 зависит от двух внешних воздействий:
1. ДВС. Из структурной схемы ДВС (рис. 5) следует, что частота вращения первичного вала w1 зависит от двух внешних воздействий: 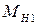 – нагрузки на первичном валу и
– нагрузки на первичном валу и 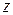 – перемещения рейки топливного насоса ДВС, изменяющего количество топлива, подаваемого в двигатель.
– перемещения рейки топливного насоса ДВС, изменяющего количество топлива, подаваемого в двигатель.
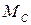 зависит от относительных дорожных сопротивлений
зависит от относительных дорожных сопротивлений 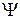 и скорости перемещения машины, т.е. от угловой скорости вращения вала вторичного
и скорости перемещения машины, т.е. от угловой скорости вращения вала вторичного 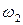 С увеличением
С увеличением 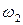 , растет ветровое сопротивление, а главное для гусеничной машины – потери в гусеничном движителе. Поэтому
, растет ветровое сопротивление, а главное для гусеничной машины – потери в гусеничном движителе. Поэтому 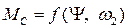 , что в линеаризованном виде соответствует выражению
, что в линеаризованном виде соответствует выражению
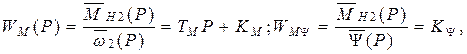 (3)
(3)


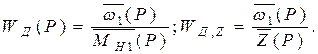
 Для получения передаточных функций запишем уравнение движения для ДВС, где искомой (выходной) функцией является управляемая величина – отклонение частоты вращения первичного вала
Для получения передаточных функций запишем уравнение движения для ДВС, где искомой (выходной) функцией является управляемая величина – отклонение частоты вращения первичного вала  от установившегося значения
от установившегося значения  :
: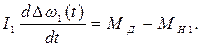
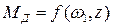 , следовательно,
, следовательно,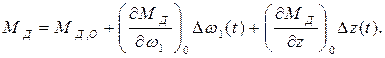
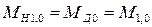 , и что
, и что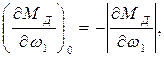
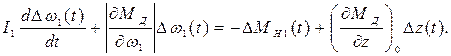
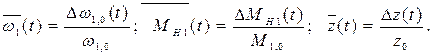

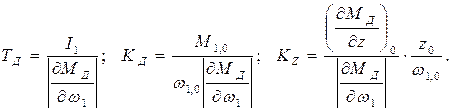
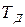 – постоянная времени двигателя, с;
– постоянная времени двигателя, с; 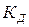 и
и  – безразмерные коэффициенты усиления.
– безразмерные коэффициенты усиления.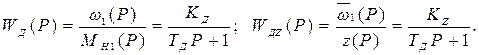
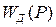 .
.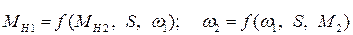
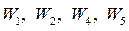 понятен, т.к. регулируемые величины меняются при изменении однородных возмущений и при перемещении органа управления передачей
понятен, т.к. регулируемые величины меняются при изменении однородных возмущений и при перемещении органа управления передачей  . Так, например, изменение
. Так, например, изменение 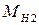 , так и изменением передаточного числа бесступенчатой передачи при перемещении
, так и изменением передаточного числа бесступенчатой передачи при перемещении 

 и
и  определяются КПД бесступенчатой передачи, как показано на рис. 7. Из рис. 7, а следует, что при очень малых частотах вращения вала гидрообъёмной бесступенчатой передачи из-за внутренних утечек масла невозможно поднять момент нагрузки на ее входном валу; при больших частотах вращения входного вала момент нагрузки также снижается из-за неудовлетворительной динамики поршневой группы и кавитационных явлений в цилиндрах поршневого блока. В связи с аналогичными причинами происходит снижение
определяются КПД бесступенчатой передачи, как показано на рис. 7. Из рис. 7, а следует, что при очень малых частотах вращения вала гидрообъёмной бесступенчатой передачи из-за внутренних утечек масла невозможно поднять момент нагрузки на ее входном валу; при больших частотах вращения входного вала момент нагрузки также снижается из-за неудовлетворительной динамики поршневой группы и кавитационных явлений в цилиндрах поршневого блока. В связи с аналогичными причинами происходит снижение 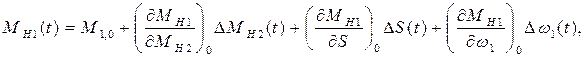
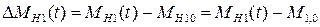 .
.


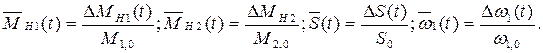

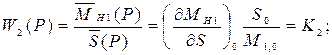
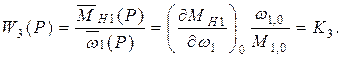
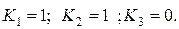
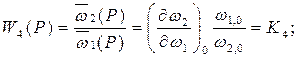
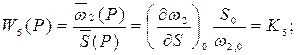
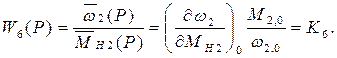
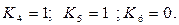
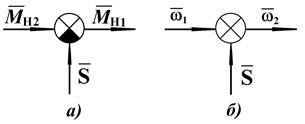

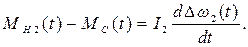
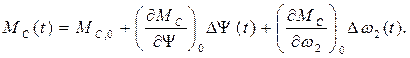
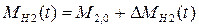 и
и 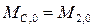 .
.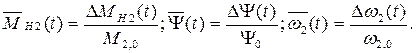
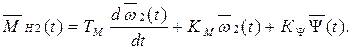
 где
где 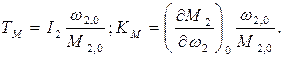
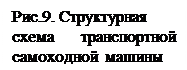 Величину
Величину 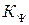 можно не определять аналитически, т.к. она характеризует нагрузку со стороны дороги и задается впоследствии независимо в виде типовых возмущений. Из выражения (3) уточняется структурная схема самоходной машины (рис.9). Из нее, в частности, следует, что нагрузка от дорожных сопротивлении
можно не определять аналитически, т.к. она характеризует нагрузку со стороны дороги и задается впоследствии независимо в виде типовых возмущений. Из выражения (3) уточняется структурная схема самоходной машины (рис.9). Из нее, в частности, следует, что нагрузка от дорожных сопротивлении 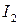 , создает нагрузку на валу машины с участием коэффициентов
, создает нагрузку на валу машины с участием коэффициентов  и
и  . Так как определение коэффициента
. Так как определение коэффициента 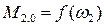 , то удобнее преобразовать выражение
, то удобнее преобразовать выражение  .
.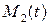 , в отличие от
, в отличие от  , переменно, с ростом
, переменно, с ростом  увеличивается в пропорции
увеличивается в пропорции 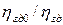 , т. е.
, т. е. 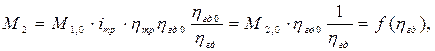
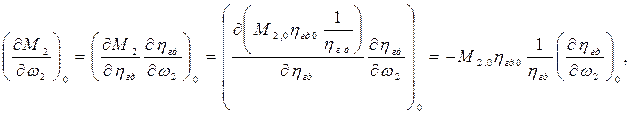
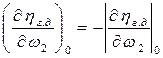 ;
;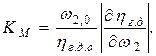 (4)
(4) , приведенному в материалах по тяговому расчету машины и по статической характеристике АС (рис.3). Если в материалах тягового расчета машины
, приведенному в материалах по тяговому расчету машины и по статической характеристике АС (рис.3). Если в материалах тягового расчета машины 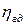 задан аналитически, математической аппроксимацией,
задан аналитически, математической аппроксимацией, 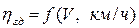 , то следует заменить в ней
, то следует заменить в ней 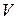 , используя
, используя  и определить частную производную
и определить частную производную 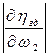 аналитически.
аналитически. 4. Регулятор центробежный. Регулируемой, выходной величиной является перемещение
4. Регулятор центробежный. Регулируемой, выходной величиной является перемещение 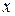 скользящей втулки регулятора, приводящее к перемещению рычага сервопривода. Возмущением является изменение скорости первичного вала
скользящей втулки регулятора, приводящее к перемещению рычага сервопривода. Возмущением является изменение скорости первичного вала 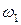 . Структурная схема центробежного регулятора показана на рис.10. Составим уравнение движения для скользящей втулки регулятора:
. Структурная схема центробежного регулятора показана на рис.10. Составим уравнение движения для скользящей втулки регулятора: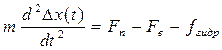 .
.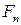 и восстанавливающей силы пружины
и восстанавливающей силы пружины 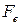 введена сила гидравлического трения скользящей втулки
введена сила гидравлического трения скользящей втулки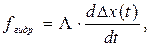
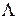 – коэффициент демпфирования;
– коэффициент демпфирования;  – масса всех деталей, в том числе и грузовых звеньев регулятора, приведенная к скользящей втулке. Значение поддерживающей и восстанавливающей сил:
– масса всех деталей, в том числе и грузовых звеньев регулятора, приведенная к скользящей втулке. Значение поддерживающей и восстанавливающей сил: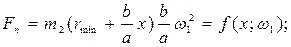
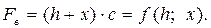
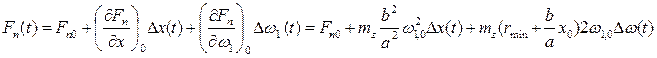
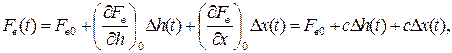
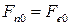 .
.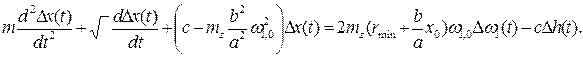
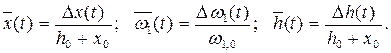
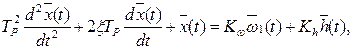
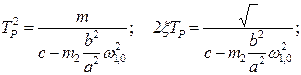
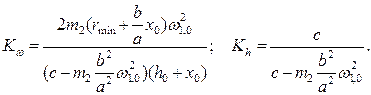 (5)
(5)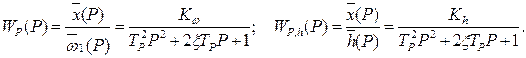
 регулятора постоянна и регулятор описывается одной передаточной функцией
регулятора постоянна и регулятор описывается одной передаточной функцией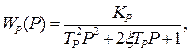
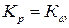 .
.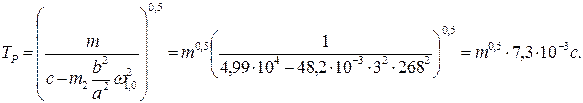
 на несколько порядков меньше времени процессов управления АС, то можно рассматривать регулятор как пропорциональное звено, т.е., принимая
на несколько порядков меньше времени процессов управления АС, то можно рассматривать регулятор как пропорциональное звено, т.е., принимая 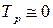 , можно полагать
, можно полагать 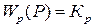 . Более удобно для расчетов
. Более удобно для расчетов  выражение
выражение 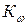 из (5) преобразовать следующим образом:
из (5) преобразовать следующим образом: (6)
(6)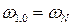

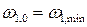
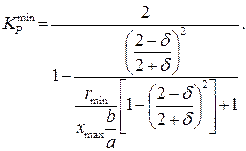
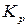 по параметрам заданий на проектирование АС меняется в пределах
по параметрам заданий на проектирование АС меняется в пределах 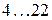 . Бó льшие значения
. Бó льшие значения 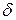 .
.
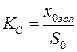 – отношение номинальных (нулевых) значений перемещений золотника и поршня, т. е. отношение их представляющих параметров, постоянная времени сервопривода:
– отношение номинальных (нулевых) значений перемещений золотника и поршня, т. е. отношение их представляющих параметров, постоянная времени сервопривода: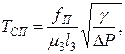
 где
где  – площадь поршня, м3;
– площадь поршня, м3;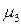 – коэффициент расхода жидкости через золотники,
– коэффициент расхода жидкости через золотники,  ;
;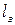 – ширина окна золотникового отверстия, м;
– ширина окна золотникового отверстия, м;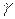 – плотность рабочей жидкости, Н/м3;
– плотность рабочей жидкости, Н/м3;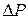 – суммарный перепад давлений, заставляющий поршень перемещаться, Па.
– суммарный перепад давлений, заставляющий поршень перемещаться, Па. определяется практически соотношением площади поршня и проходного сечения золотника.
определяется практически соотношением площади поршня и проходного сечения золотника.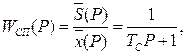
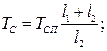
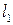 – расстояние между осями золотника и поршня;
– расстояние между осями золотника и поршня;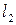 – расстояние между осями золотника и скользящей муфты регулятора.
– расстояние между осями золотника и скользящей муфты регулятора.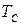 , которая обеспечит минимальное время
, которая обеспечит минимальное время  переходного процесса
переходного процесса  исследуемой АС.
исследуемой АС.


