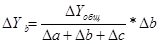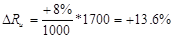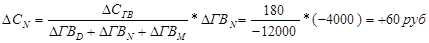Способ пропорционального деления и долевого участия
В ряде случаев для определения величины влияния факторов на прирост результативного показателя может быть использован способ пропорционального деления. Это касается тех случаев, когда мы имеем дело с аддитивными моделями Y= а _. Y = а + Ь + с +... + п b + c + d +... + п к В первом случае, когда имеем одноуровневую модель типа Y= a + b + с, расчет проводится следующим образом:
110 Т
Например, уровень рентабельности повысился на 8% в связи с увеличением суммы прибыли на 1000 тыс. руб. При этом прибыль возросла за счет увеличения объема продаж на 500 тыс. руб., за счет роста цен — на 1700 тыс. руб., а за счет роста себестоимости продукции снизилась на 1200 тыс. руб. Определим, как изменился уровень рентабельности за счет каждого фактора:

Методика расчета для смешанных моделей несколько сложнее. Взаимосвязь факторов в комбинированной модели можно проиллюстрировать (рис. 5.1). Установлено, что за счет снижения среднегодовой выработки автомобиля себестоимость 1 ткм повысилась на 180 руб. При этом известно, что выработка снизилась: а) из-за сверхплановых простоев машин — на 5000 ткм; б) сверхплановых холостых пробегов —на 4000 ткм; в) неполного использования грузоподъемности —на 3000 ткм. Всего — на 12 000 ткм. Отсюда можно определить изменение себестоимости под влиянием факторов второго уровня:
Всего + 180 руб. Для решения такого типа задач можно использовать также способ долевого участия. Для этого сначала определяется доля каждого фактора в общей сумме их приростов, которая затем умножается на общий прирост результативного показателя (табл. 5.5):
Таблица 5.5
Рис. 5.1. Схема взаимодействия факторов Расчет влияния факторов на результативный показатель способом долевого участия
112 113
Элиминирование как способ детерминированного факторного анализа имеет существенный недостаток, поскольку предполагает, что факторы изменяются независимо друг от друга. На самом же деле они изменяются совместно, взаимосвязанно, и от этого взаимодействия получается дополнительный прирост результативного показателя, который при использовании способов цепной подстановки, индексного метода, абсолютных и относительных разниц присоединяется к последнему фактору. В связи с этим размер влияния факторов на изменение результативного показателя меняется в зависимости от места, которое занимает тот или иной фактор в детерминированной модели. Согласно приведенным в табл. 5.1 данным количество рабочих на предприятии увеличилось на 20%, производительность труда — на 25%, а объем производства продукции — на 50%. Это значит, что 5% (50 - 20 - 25), или 20 млн руб. валового выпуска продукции, составляет дополнительный прирост от взаимодействия обоих факторов. Когда мы подсчитаем условный объем выпуска продукции исходя из фактического количества рабочих и базисного уровня производительности труда, весь дополнительный прирост от взаимодействия двух факторов будет отнесен к качественному фактору — изменению производительности труда: ВП0 = ЧР0 ■ ГВ0 = 100 ■ 4 = 400 млн руб.; ВПусл = ЧР{ ■ ГВ0 =!20 ■ 4 = 480 млн руб.; ВП1 = ЧРХ ГВХ = 120-5 = 600 млн руб.; АВПчр = ВПус1 - ВЛ0 = 480 - 400 = +80 млн руб.; АВПГВ = ВПХ - ВПусл = 600 -480 = +120 млн руб. Если при расчете условного объема ВП использовать количество рабочих базисного периода и уровень производительности труда отчетного периода, то весь дополнительный прирост продукции будет отнесен к количественному фактору, который мы изменяем во вторую очередь: ВП0 = ЧР0 ■ ГВ0 = 100 4 = 400 млн руб.; ВПусл = ЧРo ■ ГВ1 = 100 ■ 5 = 500 млн руб.; ВПХ = ЧР1 ■ ГВ1 = 120- 5 = 600 млн руб.; - АВПчр = ВПХ - ВПусл = 600 -500 = +100 млн руб.; АВЛГВ = ВПусл - ВП0 = 500 - 400 = +100 млн руб.
Графическое решение задачи в разных вариантах приведено на рис. 5.2.
Рис. 5.2. Графическое решение задачи деления дополнительного прироста при использовании способов элиминирования В первом варианте расчета условный показатель имеет форму ВПусл=ЧР1ГВ0 во втором — ВПусл=ЧРо*ГВ1. Соответственно, отклонения за счет каждого фактора в первом случае ΔВПчр = ΔЧР ГВ0; ΔВПГВ = ЧРХ ■ ΔГВ; во втором — ΔВПчр = ΔЧРГВХ; ΔВПГВ = ЧР0 ■ ΔГВ На графиках этим отклонениям соответствуют разные прямоугольники, так как при разных вариантах подстановки величина дополнительного прироста результативного показателя, равная прямоугольнику ABCD, относится в первом случае к величине влияния годовой выработки, а во втором — к величине влияния количества рабочих. В результате размер влияния одного фактора преувеличивается, а другого — преуменьшается. Это вызывает неоднозначность оценки влияния факторов, особенно в тех случаях, когда дополнительный прирост довольно существенный, как в нашем примере. Чтобы избавиться от этих недостатков, в детерминированном факторном анализе используют интегральный метод, метод логарифмирования и др.
114 115
|

 и моделями кратно-аддитивного типа:
и моделями кратно-аддитивного типа: